Программирование векторных и матричных операций

Лабораторная рАбота  №1

Тема:    Программирование векторных и матричных операций.

Цель:   Научиться программировать векторные и матричные операции и создать библиотеку процедур и функций, которые реализуют эти операции в последующих лабораторных работах.

Задание:

1. Разработать процедуры или функции, которые реализуют следующие операции:

а) произведение вектора и скаляра;

б) сумма двух векторов;

в) скалярное произведение векторов;

г) произведение матрицы на число;

д) произведение матрицы на вектор;

е) суммы двух матриц;

ё) разность двух матриц;

ж) произведение двух матриц.

2. Разработать программу, которая позволяет вводить значение матрицы векторов, и выполнять тестирование.

3. Выполнить действия над матрицами: (А – В) (А + В) – 2АВ

                 

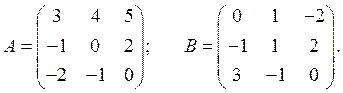
Теоретическая часть работы

Методика решения:

К линейным дей­ствиям над векторами относятся: их сложе­ние (и связанное с ним вычитание) и умно­жение вектора на скаляр.

1. При сложении векторов их координаты склады­ваются, т.е.

если а = а₁ + а₂, то X = X₁ +X₂, Y = Y₁ + Y₂, Z = Z₁ + Z₂.

2. Аналитическое правило для вычитания векторов:

если а = а₁ – а₂, то X = X₁ –X₂, Y = Y₁–Y₂, Z = Z₁–Z₂

3. При умножении вектора на число все координа­ты множатся на то же число, т.е.

если m₂ = λm₁, то Х₂ = λХ₁, Y₂ = λY₁, Z₂ = λZ₂.

Скалярным произведением вектора а на вектор b называется произведение их модулей на косинус угла между ними. Sk= | а| • | b| cos().

Модуль – длина вектора а {X, У, Z} выражается через его ко­ординаты

формулой 

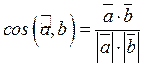Матрицей А размера – прямоугольная таблица из m строк и n столбцов состоит из чисел и других математических выражений  (элементами матрицы)

Существует такие действия с матрицей как: сложение, вычитание, умножение и умножение матрицы A на число m. 

Даны две матрицы:

A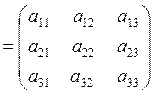и B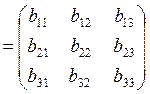

Суммой двух матриц Аи В называется матрица, определяемая равенством:

A + B

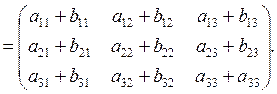
Произведением числа т на матрицуAназывается матрица, определяемая равенством:

mA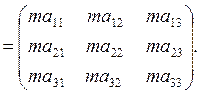

Произведение двух матриц A иBобозначается символом АВ и определяется равенством:

AB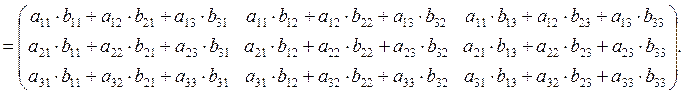

Произведениемматрици(размеромисоответственно) называется матрица С размера , если

Классификация данных:

Начальные данные	Переменная
	Имя	Тип	Значение
	1..Matrix_Size	Целочисленный	Строка матрицы А
	1..Matrix_Size	Целочисленный	Столбец матрицы А
	1..Matrix_Size	Целочисленный	Строка матрицы Б
	1..Matrix_Size	Целочисленный	Столбец матрицы Б
3	Matrix_Size	Целочисленный	Строка и столбец матриц А и Б
3	Vector_Size	Целочисленный	Размер вектора
	1..Vector_Size	Целочисленный	Вектор
0	Matrix_A	MatrixArray	Содержит  значение матрицы А
0	Matrix_B	MatrixArray	Содержит  значение матрицы Б
0	MatrixRes_1	MatrixArray	Содержит  результат действий над  матрицами
0	MatrixRes_2	MatrixArray	Содержит  результат действий над  матрицами
0	Vector_A,	VectorArray
0	Vector_B	VectorArray
0	VectorRes_1	VectorArray	Содержит  результат действий над  векторами
0	VectorRes_2	VectorArray	Содержит  результат действий над  векторами
‘’	File_Input1	Строковый	Содержит имя файла на диске
‘’	File_Input2	Строковый	Содержит имя файла на диске
'Output.txt'	File_Output	Строковый	Содержит имя файла на диске
‘’	Input	Строковый	Содержит имя файла на диске
	File_On_Disk	Текстовый	Указатель на  файл

Текст программы:

Текст основной программы:

Program LR1;

uses

  crt, U_MATRIX, U_putDat, U_Vector;

var

  Matrix_A,Matrix_B,MatrixRes_1,MatrixRes_2: MatrixArray;

  Vector_A, Vector_B,VectorRes_1,VectorRes_2: VectorArray;

  File_Input1,File_Input2,File_Output, Input: string;

  Sc:Integer;  ch: char; File_On_Disk:text;

BEGIN

  ClrScr;

  File_Output := 'Output.txt';

  WriteLn('Vector A:');

  Data_to_Vector(Vector_A,Vector_Size);

  WriteLn('Vector B:');

  Data_to_Vector(Vector_B,Vector_Size);

  ClrScr;

  WriteLn('Matrix A:');

  Data_to_Matrix(Matrix_A,Matrix_Size);

  WriteLn('Matrix B:');

  Data_to_Matrix(Matrix_B,Matrix_Size);