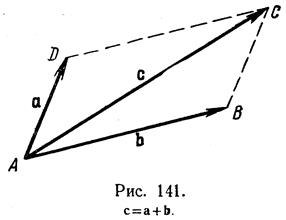
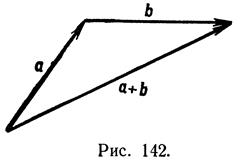
концу первого вектора надо приставить начало второго; тогда суммой будет служить замыкающий вектор, т. е. идущий от начала первого в конец второго рис. 142. Если теперь к этой сумме требуется прибавить некоторый третий вектор, то его надо приставить к концу второго вектора и взять замыкающий и т. д.
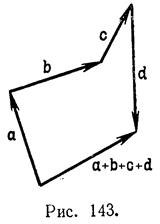
Общее правило сложения любого числа векторов проиллюстрировано на рис. 143.
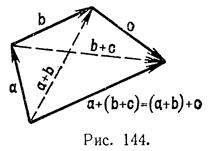
Из рис. 144 вытекает, что справедлив сочетательный закон а + (b + с) = (а + Ь) + с, который вместе с переместительным законом показывает, что при сложении любого числа слагаемых их порядок и расстановка скобок несущественны, например:
(a + b) + (c + d) = [(b + d) + c] + a = [c + (a + d)] + b ит.п.
Подчеркнем, что сложение векторов различной размерности, а также сложение вектора и скаляра невозможны] кроме того, в нашем курсе векторы не сравниваются друг с другом — не будет положительных и отрицательных векторов, неравенств вида а>b и т. д. Конечно, модули (длины) векторов сравнивать друг с другом можно, но не следует удивляться, если модуль суммы векторов окажется меньшим, например, чем модули каждого из слагаемых: ведь векторы складываются не как числа, а как силы, и может оказаться, что равнодействующая нескольких сил окажется меньше, чем каждая из этих сил.
Заметим в заключение следствие из рис. 143:
| a + b + c + d | ≤ | a | + | b | + | c | + | d |;
при этом равенство получится, если все слагаемые векторы одинаково направлены; тогда, если их приставить один к другому, они будут продолжать друг друга по прямой.
1. При сложении векторов их координаты складываются, т. е. если а = а1 + а2, то X = X1 + Л2, Y = Y1 + К2, Z = Z1 + Z2.
2. Аналитическое правило для вычитания векторов: если а = а1 – а2, то X = X1– Л2, Y = Y1– К2, Z = Z1–Z2
3. При умножении вектора на число все координаты множатся на то же число, т. е. Если m2 = λm1, то Х2 = λХ1, Y2 = λY1, Z2 = λZ2.
Если векторы a1{Х1, Y1, Z1,}, a2{Х2, Y2, Z2,}, коллинеарны, то их соответственные координаты пропорциональны:
Х2 : X1 = Y2 : Y1 = Z2 : Z1 (1)
и обратно.
Если коэффициент пропорциональности 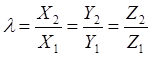 положителен, то векторы а1и а2 равнонаправлены;если отрицателен —
противоположно направлены. Абсолютное значение λ выражает отношение длин | а2 | : | а1
|.
положителен, то векторы а1и а2 равнонаправлены;если отрицателен —
противоположно направлены. Абсолютное значение λ выражает отношение длин | а2 | : | а1
|.
Замечание. Если одна из координат вектора а1 равна нулю, то пропорцию (1) надо понимать в том смысле, что соответствующая координата вектора а2 тоже равна нулю.
Три вектора (или большее число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.
Если хотя бы один из трех векторов — нулевой, то три вектора тоже считаются компланарными.
Признак компланарности см. в §§ 116, 120.
Модуль – длина вектора а {X, У, Z} выражается через его координаты формулой
| а | = ![]() (1)
(1)
Расстояние dмежду точками А1 (x1; y1; z1;); A2 (х2; y2; z2;) представляется формулой
d =![]() (2)
(2)
Она получается из (1) в силу формул (2) .
Пример 2. Расстояние между точками А1 (8;— 3; 8), A2 (6; -1; 9) есть
d =![]() .
.
Угол между осью координат и вектором.
Углы![]() (черт. 149), образуемые
положительными направлениями OX, OY, OZс вектором
а {X,Y,Z}, можно найти по формулам (Из прямоугольного треугольника OMR имеем:
(черт. 149), образуемые
положительными направлениями OX, OY, OZс вектором
а {X,Y,Z}, можно найти по формулам (Из прямоугольного треугольника OMR имеем: 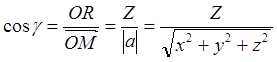 ).
).
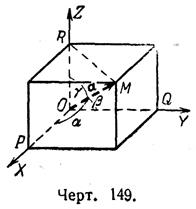
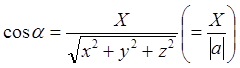 (1)
(1)
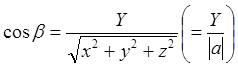 (2)
(2) 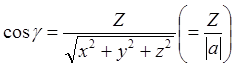 (3)
(3)
Если вектор a имеет длину, равную единице масштаба, т.е. если | а | = 1, то
![]()
Из (1),(2),(3) следует:
![]() (4)
(4)
Аналогично получаются формулы (1) и (2).
Скалярным произведением вектора а на вектор b называется произведение их модулей на косинус угла между ними.
Обозначение: a• bили аb.
Согласно определению
ab= | а
| • | b| cos(![]() ). (1)
). (1)
В силу теоремы 2 | b | cos(![]() ) = праb, так что
вместо (1) можно написать:
) = праb, так что
вместо (1) можно написать:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.