

Завдання 1.
Дано:
Дослідити збіжність
числового ряду![]() :
:
а) знакосталого
– 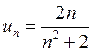 ; б) знакозмінного
–
; б) знакозмінного
– 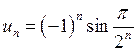 .
.
Для знакозмінного ряду, якщо він збігається, визначити, яка збіжність має місце – абсолютна чи умовна.
Решение:
а) знакосталого
–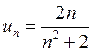 ;
; 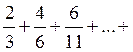 ; сравниваем данный ряд с гармоническим, расходящимся радом
; сравниваем данный ряд с гармоническим, расходящимся радом ![]() ;
; 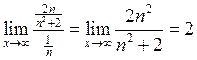 ; так
как 2 > 0 значит ряд расходящийся.
; так
как 2 > 0 значит ряд расходящийся.
б)
знакозмінного – 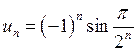 ;
; 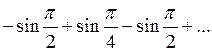 ; по условиям теоремы Лейбница
данный рад сходящийся:
; по условиям теоремы Лейбница
данный рад сходящийся:
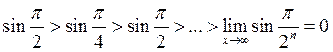 ;
;
Сравним этот ряд с сходящимся
рядом 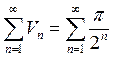 ;
; 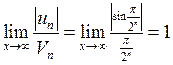 ; так
как 1 > 0 значит ряд из абсолютных членов сходящийся, а значит
знакопеременный ряд – абсолютно сходящийся.
; так
как 1 > 0 значит ряд из абсолютных членов сходящийся, а значит
знакопеременный ряд – абсолютно сходящийся.
Завдання 2.
Дано:
Визначити область
збіжності степеневого ряду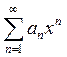 .
.
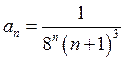 .
.
Решение:
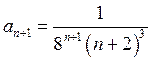 ;
; 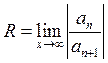 =>
=>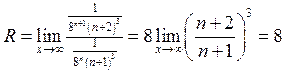 ;
;
Ряд сходится на интервале:![]() ;
;
Проверим ряд на сходимость на концах интервала;
При x=–8 ряд
имеет вид: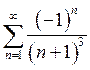 ;
;
Знакопеременный ряд является сходящимся, так как выполняет условия теоремы Лейбница:
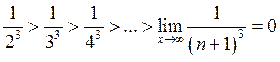
При x=8 ряд
имеет вид: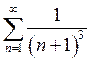 ; Сравним
полученный ряд с сходящимся рядом
; Сравним
полученный ряд с сходящимся рядом 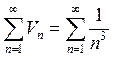
ряд является сходящимся, так как степень знаменателя больше чем 1;
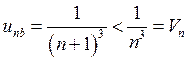 отсюда
следует то что ряд
отсюда
следует то что ряд 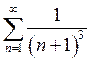 сходящийся
следовательно, следовательно степенной ряд сходится на интервале:
сходящийся
следовательно, следовательно степенной ряд сходится на интервале: ![]()
Завдання 3.
Дано:
Обчислити з точністю до 0,001 визначений інтеграл, заклавши підінтегральну функцію в степеневий ряд і потім про інтегрувавши його почленно.
Визначений
інтеграл: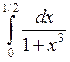
Решение:
Разлагаем функцию по формуле: ![]() ;
;
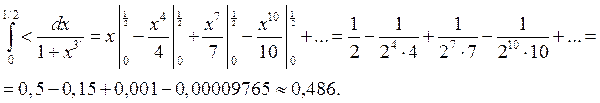
Завдання 4.
Дано:
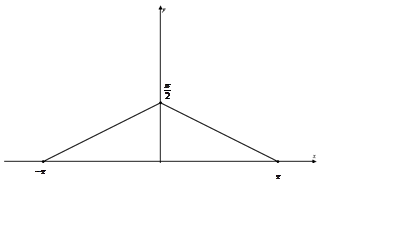
Розвинути в ряд Фур’є
функцію ![]() , задану графіком.
, задану графіком.
![]()
![]()
![]()
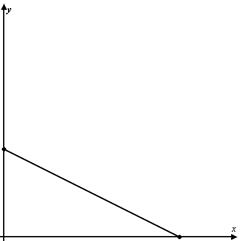
Решение:
Продлим функцию чётным образом
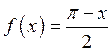 ;
; 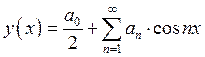 ;
;
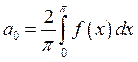 =>
=>
=>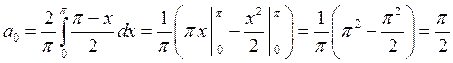 ;
;
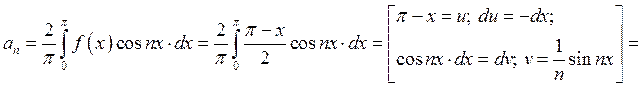
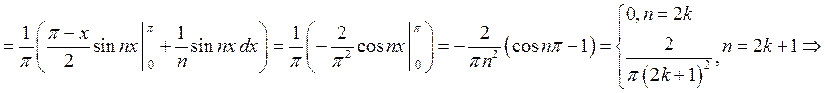
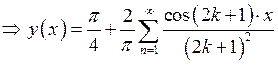 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.