Двоичная арифметика. Вычитание чисел в двоичной системе счисления

Билет 3

Двоичная арифметика.

Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.

Таблица двоичного сложения:

Таблица двоичного вычитания:

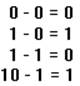
Таблица двоичного умножения:

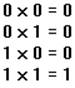
Правила арифметики одинаковы для всех позиционных систем счисления.

Сложение двух чисел в двоичной системе счисления можно выполнять столбиком поразрядно, начиная с младшего разряда, как это делается в десятичной системе счисления. В  каждом разряде, в соответствии с таблицей сложения, производится сложение двух цифр слагаемых и цифры переноса из предыдущего разряда.

Произведем сложение 55,25 и 19,5 в десятичной и в двоичной системах счисления.

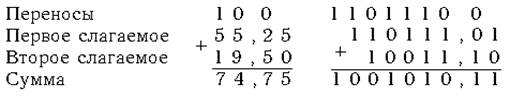
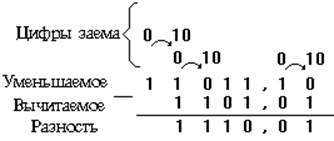
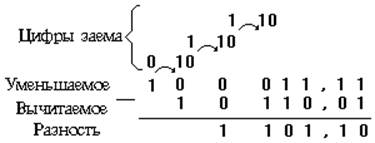
Вычитание чисел в двоичной системе счисления выполняется так же, как и в десятичной. При вычитании  в данном разряде занимается единица из следующего старшего разряда. Причем, занимаемая  единица  равна  двум единицам данного  разряда. Следует отметить, что в десятичной системе счисле-ния занимаемая единица равна десяти единицам данного раз-ряда. Заем единицы производится каждый раз, когда цифра в разряде вычитаемого количественно больше цифры в том же разряде уменьшаемого.

Поясним сказанное примерами. Для лучшего уяснения рас-смотрим вычитание десятичных и двоичных чисел.

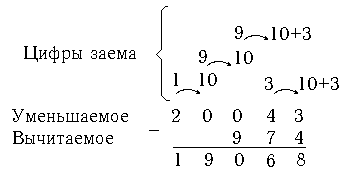
Начало стрелки в примере указывает откуда делается заем единицы. Цифра, стоящая в начале стрелки, указывает число,  оставшееся в данном разряде, а цифра в конце стрелки - чис-ло, в которое  обращается занимаемая единица.

Умножение двоичных  чисел  производится  путем образования частичных произведений и их последующего суммирования (как  и  десятичных  чисел). Например,

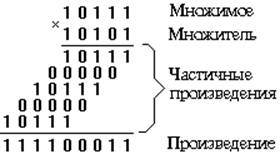
В соответствии с таблицей двоичного умножения каждое  частичное произведение или равно нулю, если в соответствующем разряде множителя стоит нуль, или равно множимому, если в соответствующем разряде множителя стоит единица.

При сложении частичные произведения сдвигаются так, что младшие разряды их совпадают с разрядами множителя, от которых получены эти частичные произведения.

Таким образом, операция умножения двоичных чисел сводится к операции сдвига и сложения. Положение запятой определяется  так  же,  как  при умножении десятичных чисел.

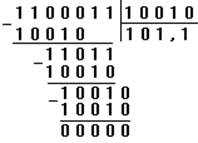
Деление чисел в двоичной системе счисления производится аналогично делению десятичных чисел. При делении нецелых чисел, они могут быть приведены к целым путем переноса запятой в делимом и делителе на одинаковое число  разрядов и дописывания нулей в недостающие справа разряды. Например,