Исследование спектров частотно-модулированных колебаний.
Цель лабораторной работы
Целью лабораторной работы является изучение спектрального состава частотно-модулированныхсигналов.
Теоретические основы лабораторной работы
Несущее колебание может передавать полезную информацию изменением частоты или фазы или амплитуды. При частотной модуляции изменяется частота несущего колебания по закону модулирующего сигнала.
![]()
Положим j(t) = 0.
![]()
w0 - частота несущего колебания;
![]() - максимальное отклонение частоты, или девиация.
- максимальное отклонение частоты, или девиация.
Значение углового аргумента несущего колебания связано с меняющейся частотой
|
|
Примем ![]()
Тогда выражение для частотной модуляции будет иметь вид
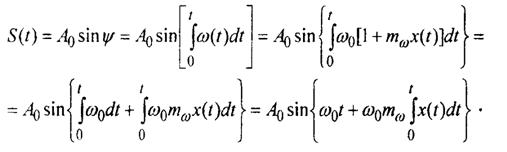
В качестве простейшего модулирующего сигнала, представляющего полезную информацию, примем гармонический (тональный) низкочастотный сигнал:
![]()
Получим новое выражение для частотной модуляции
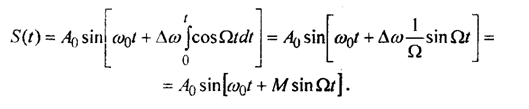
Здесь: ![]() - индекс модуляции, показывающий
максимальное отклонение частоты несущего колебания при заданном (обычно 1000
Гц) значении частоты модулирующего колебания.
- индекс модуляции, показывающий
максимальное отклонение частоты несущего колебания при заданном (обычно 1000
Гц) значении частоты модулирующего колебания.
Преобразуем выражение для частотной модуляции (для синуса суммы двух углов):
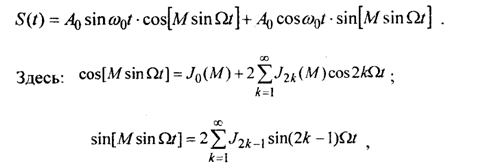
где Jn (М) - формула Бесселя n-го порядка от аргумента -М. График нормированных функций Бесселя приведен на рис. 19 (см. табл. 1).
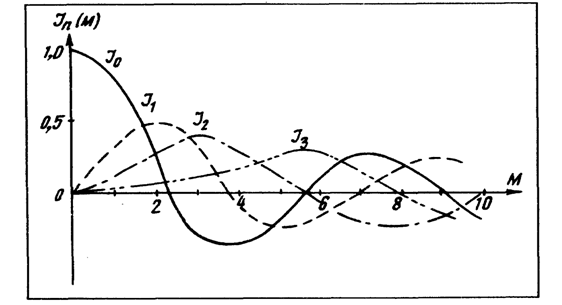
Рис. 19
Таблица 1
|
М |
j0 |
J1 |
J2 |
J3 |
J4 |
|
0,0 |
+1,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
0,5 |
+0,94 |
+0,24 |
+0,01 |
+0,00 |
+0,00 |
|
1.0 |
+0,76 |
+0,44 |
+0,11 |
+0,02 |
+ 0,002 |
|
2,0 |
+0,22 |
+0,58 |
+0,35 |
+0,13 |
+ 0,003 |
|
3,0 |
-0,26 |
+0,34 |
+0,48 |
+0,31 |
+0,13 |
|
4,0 |
-0,39 |
-0,06 |
+0,36 |
+0,43 |
+0,28 |
|
5,0 |
-0,18 |
-0,33 |
+0,04 |
+0,36 |
+0,39 |
|
10,0 |
-0,25 |
+0,04 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.