МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”
КАФЕДРА ОБЧИСЛЮВАЛЬНОЇ ТЕХНІКИ ТА ПРОГРАМУВАННЯ
Лабораторна робота №1
з курсу "Інтелектуальні комп’ютерні системи"
за темою: " Розпізнавання зображень по куту між векторами, скалярному добутку й по приналежності до заданої області простору "
Виконал:
ст групи КІТ -14б
Богачов О. С.
Мета: Придбання й закріплення знань і одержання практичних навичок роботи з найпростішими алгоритмами розпізнавання на основі подання зображень у вигляді крапок або векторів в n-мірному векторному просторі.
Індивідуальне завдання:
1. Розробити алгоритм і програму, що моделює розпізнавання різних об'єктів в n-мірному векторному просторі по куті між векторами й скалярним добутком.
2. Задатися розмірністю n-мірного векторного простору, числом m еталонних об'єктів образів (n і m повинні бути не менш 5) і декількома розпізнаваними об'єктами. За допомогою кута між векторами й скалярним добутком визначити приналежність пред'явлених об'єктів до того або іншого образа.
3. Розробити алгоритм і програму, що моделює розпізнавання різних об'єктів по їхній приналежності до кулястих або конусоподібних областей в n-мірному векторному просторі.
4. Задатися розмірністю n-мірного векторного простору, числом m образів і декількома розпізнаваними об'єктами. Визначити приналежність пред'явлених об'єктів до того або іншого образа при кулястих і конусоподібних областях, що містить зображення заданих образів.
Хід роботи:
У даній лабораторній роботі розглядається безперервний n-мірний векторний простір. Міра подібності зображень в n-мірному векторному просторі вводиться як функцію двох змінних L(Sk, Si), де Sk, Si Î S; S = {S1, S2, …, Sn} - кінцева безліч зображень у розглянутому просторі.
В n-мірному просторі міра подібності зображень може бути уведена багатьма способами. У даній лабораторній роботі розглядаємо розпізнавання:
- по куту між векторами;
- по скалярному добутку;
- по приналежності до заданої області простору.
При розпізнаванні по куту між векторами, якщо задано вхідне зображення Sі = (sі1, sі2, ..., sіn) і вектори еталонних зображень X1 = (x11, x12, ..., x1n), X2 = (x21, x22, ..., x2n), ..., Xm = (xm1, xm2, ..., xmn), то міра подібності між вхідним і еталонним зображеннями визначається виразом:
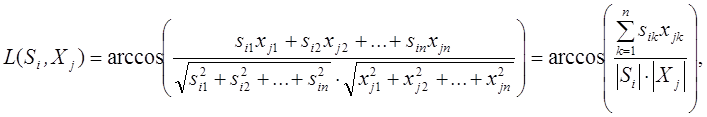
Приналежність вхідного зображення Sі до одному з m образів визначається за допомогою вирішального правила
![]()
Розпізнавання зображень по скалярному добутку 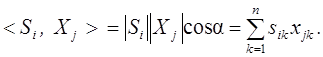 проводиться так:
проводиться так: 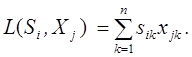
У цьому випадку приналежність вхідного зображення Sі до якого-небудь образа визначається за допомогою вирішального правила
![]()
Розпізнавання зображень по приналежності до заданої
області простору: весь простір зображень V розбивається на непересічні області
V1, V2, ..., Vm, Vm+1, де V1,
V2, ..., Vm- області, що містять зображення тільки одного
відповідного образа X1, X2, ..., Xm; Vm+1 -область,
що не містить зображень, що ставляться до зазначених образів. У цьому випадку
приналежність вхідного зображення Sі = (sі1, sі2, ...,
sіn) до деякому j-му образу визначається вирішальним
правилом ![]()
На даному рисунку видно, що задано два еталони А та В, англійські букви РО, у якості вхідного зображення С вводимо літеру О. При обчисленні за формулами отримуємо результат: І за скалярним добутком. І за кутами між векторами вхідне зображення подібне еталону В, що є вірним.
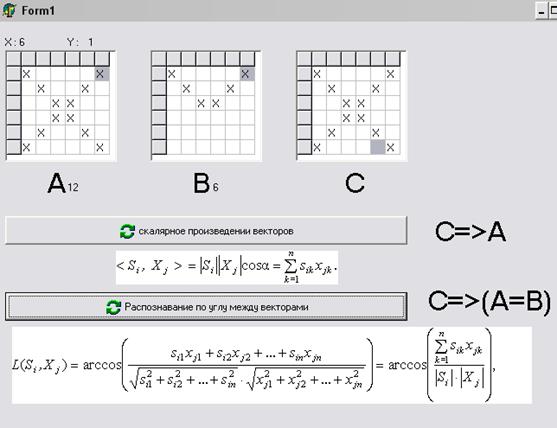
Рисунок 1.
Для наглядності введемо інше зображення, яке має подібний вигляд, але не точно збігається з еталоном:
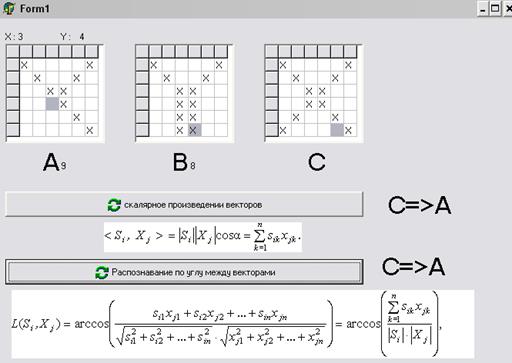
Рисунок 2.
По результатам видно, що обидві формули визначили належність вхідного зображення до еталону А. Але є і такий випадок, коли різні методи обчислення дають різні результати. Так, наприклад, як наведено на рисунку 3, вхідне зображення має нечіткий вигляд і рішення за допомогою кута між векторами дає результат, що С є приближеною до еталону В, а розпізнавання зображень по скалярному добутку дає висновок, що вхідне зображення відповідає обом еталонам одночасно.
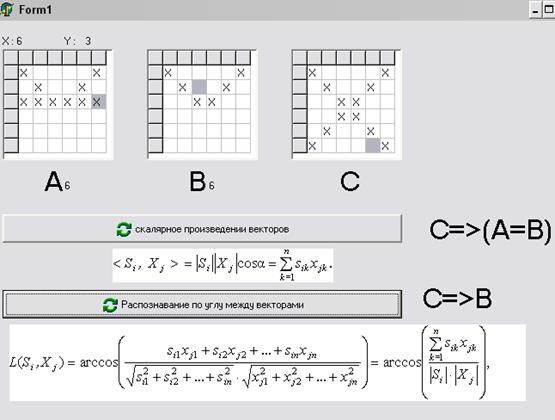
Рисунок 3.
Висновок: в результаті лабораторної роботи були придбані й закріплені знання і одержані практичні навички роботи з найпростішими алгоритмами розпізнавання на основі подання зображень у вигляді векторів в n-мірному векторному просторі.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.