МІНІСТЕРСТВО ОСВІТИ Й НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
"ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ"
Звіт з лабораторної роботи №6
"Символічни обчислення в MatLab"
за курсом "Математичні пакети"
Виконав
ст. гр. КІТ-14в
Богачов О. С.
ХАРКІВ - 2006
Лабораторна робота № 6
Тема: Символічни обчислення в MatLab
мета: Одержання практичних навичок роботи з пакетом MatLab при обчисленні в символічному вигляді.
Хід роботи
1. Задаю за допомогою символічних змінних дві символічні матриці A і B, розмірами 3*3. Визначите добуток матриць A і B.
>> syms a b c d e f g h i
>> A=[a b c;d e f;g h i]
A =
[ a, b, c]
[ d, e, f]
[ g, h, i]
>> B=[i h g;f e d;c b a]
B =
[ i, h, g]
[ f, e, d]
[ c, b, a]
>> C=A*B
C =
[ i*a+b*f+c^2, a*h+b*e+c*b, a*g+b*d+c*a]
[ i*d+e*f+f*c, d*h+e^2+b*f, d*g+e*d+f*a]
[ i*g+h*f+i*c, g*h+h*e+i*b, g^2+d*h+i*a]
2. Задаю числову матрицю D, розмірами 3*3, що містить як елементи числа N, N+1, N-1, 0.9N, 2.4, 3.5 і т.д., де N Мій номер за списком у журналі групи. Одержую із числової матриці символічну.
D=[2 3 1;1.8 2.5 3.4; 6 8.7 5.89]
D =
2.0000 3.0000 1.0000
1.8000 2.5000 3.4000
6.0000 8.7000 5.8900
>> E=sym(D)
E =
[ 2, 3, 1]
[ 9/5, 5/2, 17/5]
[ 6, 87/10, 589/100]
3. За допомогою
символічних обчислень визначаю суму чисел ![]() де N Мій номер за списком у журналі групи.
де N Мій номер за списком у журналі групи.
>> c=sym('1.0e10+1.0e-10+1.0e2+1.0e-2')
c =
1.0e10+1.0e-10+1.0e2+1.0e-2
>> vpa(c)
ans =
10000000100.01000000010
4. За допомогою символічних обчислень визначаю корінь квадратний із числа N.N, із сорока двома значущими цифрами.
>> c=sym('sqrt(2.2)')
c =
sqrt(2.2)
>> vpa(c,42)
ans =
1.48323969741913258974227948816014261219598
5. Будую графіки символічних функцій:
![]() -2p < x
< 2p;
-2p < x
< 2p;
![]() , -10 £ x
£ 10; 10 £ y £ 10;
, -10 £ x
£ 10; 10 £ y £ 10;
де N мій номер за списком у журналі групи
>> f=sym('4*sin(2*x)') >> f=sym('(x-2)^2+(y-2)^3');
>> ezplot(f) >> ezplot(f,[-10 10 -10 10])
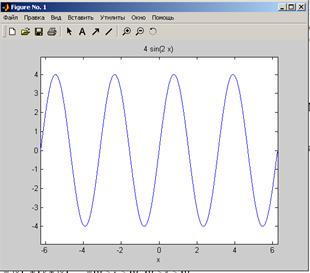
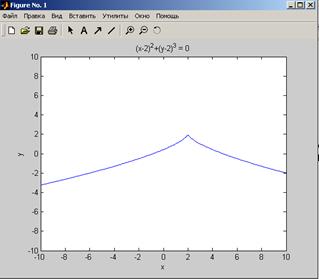
6. Поліном
, ![]() (1)
(1)
де N мій номер за списком у журналі групи,
за допомогою команди pretty відображаю в командному вікні, потім перетворюю його до виду, що містить ступеню x з відповідними коефіцієнтами.
>> p=sym('(x+N)^5-(x+2*N)^3+(x+N)^2+x-N');
>> pretty(p)
5 3 2
(x + N) - (x + 2 N) + (x + N) + x – N
>> pc=collect(p);
>> pretty(pc)
5 4 2 3 3 2
x + 5 N x + (-1 + 10 N ) x + (-6 N + 1 + 10 N ) x
2 4 5 3 2
+ (-12 N + 1 + 2 N + 5 N ) x + N - N - 8 N + N
7. Визначите коефіцієнти полінома (1) при змінної N.
>> pc=collect(p,'N');
>> pretty(pc)
5 4 2 3 3 2
N + 5 x N + (-8 + 10 x ) N + (-12 x + 1 + 10 x ) N
2 4 5 3 2
+ (-6 x + 5 x + 2 x - 1) N + x + x - x + x
>>
8. Представте поліном (1) у вигляді суми одночленів.
>> pe=expand(p);
pretty(pe)
5 4 3 2 2 3 4 5 3 2 2
x + 5 N x + 10 x N + 10 x N + 5 x N + N - x - 6 x N - 12 x N
3 2 2
- 8 N + x + 2 x N + N + x - N
9. Розкладете поліном (1) на множники.
>> p1=factor(p)
p1 =
x^5+5*N*x^4+10*x^3*N^2+10*x^2*N^3+5*x*N^4+N^5-x^3-6*x^2*N-12*x*N^2-8*N^3+x^2+2*x*N+N^2+x-N
10. Застосуєте до полінома (1) функцію horner.
>> horner(p)
ans =
(-1+(1+(-8+N^2)*N)*N)*N+(1+(2+(-12+5*N^2)*N)*N+(1+(-6+10*N^2)*N+(-1+10*N^2+(5*N+x)*x)*x)*x)*x
11. Представляю число 1000 N+2 N у вигляді добутку простих чисел.
>> a=sym('100042')
>> factor(a)
ans =
(2)*(50021)
12. Спрощую вираз
![]()
![]()
>> v=sym('sin(a)*sin(b-c)*cos(b+c-a)+sin(b)*sin(c-a)*cos(c+a-b)+sin(c)*sin(a-b)* *cos(a+b-c)')
>> pretty(v)
sin(a) sin(b - c) cos(-b - c + a) - sin(b) sin(-c + a) cos(c + a - b)+ sin(c) sin(a - b) cos(a + b - c)
>> v2=simplify(v)
v2 =
sin(a)*sin(b-c)*cos(-b-c+a)-sin(b)*sin(-c+a)*cos(c+a-b)+sin(c)*sin(a-b)*cos(a+b-c)
>> v1=simple(v)
v1 =0
13. Одержую сім
членів ряду Тейлора в околиці точки нуль для функції ![]()
>> y=sym('2*(sin(x))+cos(x)');
> tf=taylor(y, 7);
>> pretty(tf)
2 3 4 5 6
1 + 2 x - 1/2 x - 1/3 x + 1/24 x + 1/60 x - 1/720 x
14. Визначаю суму членів ряду
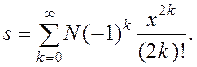
>> s=symsum((-1)^(k)*x^(2*k)/sym('(2*k)!'),k,0,inf)
s =
cos(x)
15. Визначаю ліміт 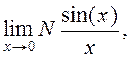 де N мій номер за списком у журналі групи.
де N мій номер за списком у журналі групи.
>> limit(2*(sin(x)/x),x,Inf)
ans =0
16. Визначаю ліміти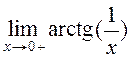 ,
, 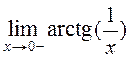 .
.
> limit(atan(1/x),x,0, 'left')
ans =-1/2*pi
>> limit(atan(1/x),x,0, 'right')
ans =1/2*pi
17. Визначаю перші три похідні від функції
![]()
де N мій номер за списком у журналі групи.
>> P=diff('2*sin(x)^2+4*x^3',x,1);
>> pretty(P)
2
4 sin(x) cos(x) + 12 x
>> P=diff('2*sin(x)^2+4*x^3',x,2);
>> pretty(P)
2 2
4 cos(x) - 4 sin(x) + 24 x
>> P=diff('2*sin(x)^2+4*x^3',x,3);
>> pretty(P)
-16 sin(x) cos(x) + 24
18. Обчислюю інтеграл
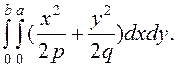
f=sym('x^2/(2*p)+y^2/(2*q)')
>> Ix=int(f,x,0,a)
Ix =
1/6/p*a^3+1/2*y^2/q*a
>> Iy=int(Ix,y,0,b)
Iy =
1/6/p*a^3*b+1/6/q*a*b^3
19. Оформив звіт по лабораторній роботі.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.