МІНІСТЕРСТВО ОСВІТИ Й НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
"ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ"
Звіт з лабораторної роботи №5
"М-файли й основи програмування в MatLab"
за курсом "Математичні пакети"
Виконав
ст. гр. КІТ-14в
Марченко В.Ю.
ХАРКІВ - 2006
Лабораторна робота № 5
Тема: М-файли й основи програмування в MatLab
мета: Одержання практичних навичок роботи з пакетом MatLab при використанні М-файлів і виконанні програм з нелінійною структурою.
Хід роботи
1. Створюю М-файл mydemo.m.
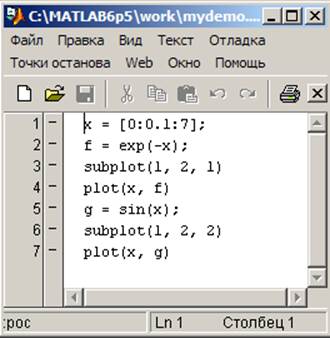
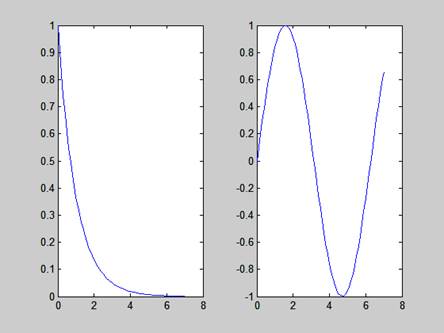
2. Створюю у кореневому каталозі диска D каталог зі своїм прізвищем (WORK_Marchenko), і записую туди М-файл mydemo.m. Встановлюю шляхи до файлу й демонструю доступність файлу з командного рядка.
path('D:\Work_Marchenko',path)
mydemo
3. Із графіки файлу-функції myfun за допомогою команд plot і fplot на одних осях (за допомогою hold on).
4. З файл-функцію root2, що знаходить тільки речовинних корінь квадратного рівняння, а при наявності комплексних корінь видає повідомлення про помилку. У демонстраційних прикладах другий коефіцієнт квадратного рівняння повинен бути дорівнює Вашому номеру за списком у журналі групи.
5. З файл-функцію, що знаходить найбільший загальний дільник (НОД) z двох натуральних чисел x і y за допомогою алгоритму Евклида. В одному з демонстраційних прикладів найбільший загальний дільник повинен бути дорівнює 3N+1, де N Ваш номер за списком у журналі групи.
Довідкова інформація. Ідея алгоритму Евклида заснована на тім, що якщо НОД те при рівності чисел x і y НОД z збігається с x и y, а у випадку нерівності чисел x і y їхня різниця між більшим і меншим разом з меншим числом має той же самий найбільший загальний дільник. Алгоритм визначення НОД Евклида можна записати в такий спосіб:
Крок 1. Якщо x > y, то перейти на крок 2.
Крок 2. Якщо x < y, то перейти на крок 5, інакше перейти на крок 3.
Крок 3. z = x. Кінець.
Крок 4. Від x відняти y і вважати, що ця різниця тепер дорівнює значенню x. Перейти на крок 1.
Крок 5. Від y відняти x і вважати, що ця різниця тепер дорівнює значенню y. Перейти на крок 1.
6. Напишіть файл-функцію, що знаходить прості числа, що не перевершують 150+10N, де N Ваш номер за списком у журналі групи.
Довідкова інформація. Простими називаються цілі позитивні числа, більші одиниці, які без залишку діляться тільки на самих себе й одиницю. Одним з найбільш простих алгоритмів одержання простих чисел, що не перевершують n, є алгоритм Эратосфена, що одержав назву решета Эратосфена. Він складається з наступних кроків:
Крок 1. Виписати послідовно всі цілі числа, починаючи із двох і кінчаючи n.
Крок 2. Уважати, що значення імені p дорівнює двом.
Крок 3. Якщо , то перейти на крок 4, інакше перейти на крок 6.
Крок 4. У послідовності чисел, починаючи із числа p + 1, закреслити кожне p-і число (тобто закреслити всі числа, кратні p, не обертаючи уваги на те, що частина чисел могла бути вже закреслена).
Крок 5. Перше після числа p незакреслене число послідовності вважати новим значенням імені p. Повернутися на крок 3.
Крок 6. Процес кінчений. Всі незакреслені числа послідовності є простими.
7.Обчислите суму простих чисел, знайдених у завданні 6.
8. Оформите звіт по лабораторній роботі.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.