






Міністерство освіти і науки України
Національний технічний університет “ХПІ”
Кафедра “Обчислювальна техніка та програмування”
Лабораторна робота №2
Тема: “ Елементарний перцептрон Розенблатта ”
Виконав:
ст. гр. КІТ-14б
Ситников А.М
Перевірив:
Заковоротный А.Ю
Харків – 2008
Мета : Придбання й закріплення знань, а також одержання практичних навичок роботи з найпростішою нейронною мережею елементарний перцептрон Розенблатта
 |
Опис
Значення в кожному осередку таблиць міняються при натисканні на них мишкою з 0 в 1 або навпаки, залежно від вихідного значення. Таким чином, можлива зміна вихідних символів на інші:
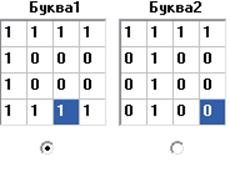
таблица весов связей перцептрона:

Вместе с таблицей весов связей перцептрона заполняется ещё таблица величин сигналов на входах:
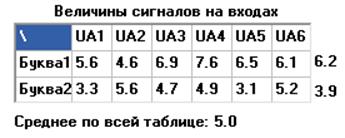
Значення цієї таблиці прямо залежать від уведених символів і від значень таблиці ваг зв'язків перцептрона. Тому необхідно підбирати останню для одержання найкращого результату величин сигналу на входах. А елементів, результат повинен бути таким:
1. Хоча б одне значення в стовпці матриці повинне бути більше або дорівнює значенню порога ("середнє по всій таблиці" наведено під таблицею величин сигналів на входах).
2. Області вище порога для різних символів повинні перетинатися якнайменше раз.
Наприклад:
В отриманій нами таблиці величин сигналів на входах хоча б одне значення стовпця вище (або дорівнює) значення порога й області вище порога перетинаються тільки в одному місці (UA4):
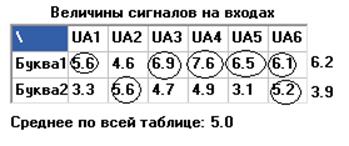
где ![]() - значення, що входить в область
значень, які вище порога .
- значення, що входить в область
значень, які вище порога .
При підборі таблиці ваг зв'язків перцептрона для інших символів, необхідно дотримуватися того ж принципу, що різко підвищить якість розпізнання перцептроном заданих символів.
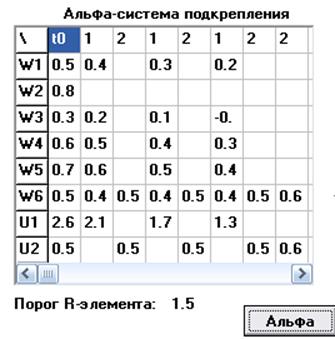
Система подкрепления даёт нам порог, в соответствии с которым есть возможность распознавать символы. Как видно из таблицы значение по первому символу (U1) ниже порога, а значение по второму (U2) – выше.
Далее можно распознавать символ с помощью альфа коррекции, введя его в
таблицу
внизу окна 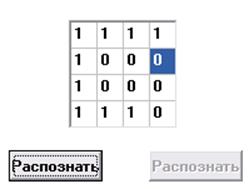 и нажав
кнопку
и нажав
кнопку ![]() , находящуюся
слева от таблицы получим результат:
, находящуюся
слева от таблицы получим результат:
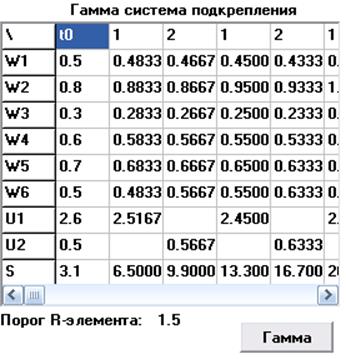
Гама система підкріплення також дає нам поріг, відповідно до якого їсти можливість розпізнавати символи. Як видно з таблиці значення по першому символі (U1) нижче порога, а значення по другому (U2) - вище (що задано крапками під символами в лівому верхньому куті форми).

Але, як було сказано на початку опису, їсти можливість міняти положення значень символу щодо порога. Дотепер розглядалася ситуація, коли значення першого символу було нижче порога, а другого - вище. Тепер розглянемо зворотну ситуацію.

Як видно з таблиці значення по першому символі (U1) стало вище порога, а значення по другому (U2) - нижче, що привело до великої кількості обчислень, і вектор t0 перетерпів значні зміни. Що однак не вплинуло на якість розпізнання символів:


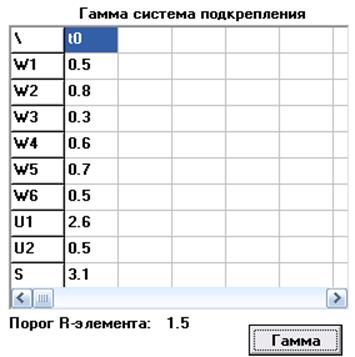
Як видно тут значення так само змінилися: по першому символі (U1) значення стало вище порога, а по другому (U2) - нижче, що привело до великої кількості обчислень, і вектор t0 так само змінився. Кількість обчислень настільки збільшилося, що довелося задіяти смугу прокручування, але це відбилося на якості розпізнання символів:
Далі можна переконається в правильності розпізнання символів:
Внешний вид программы после заполнения всех таблиц:
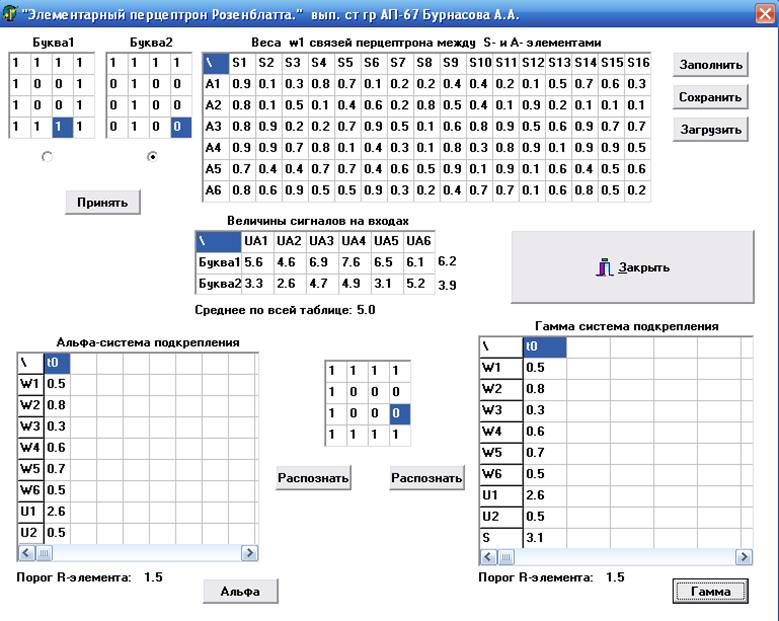
Висновок: В даній лабораторній роботі , одержали практичні навички роботи з елементарним перцептроном розенблата
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.