Подання зображень в n-мірному векторному просторі

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”

КАФЕДРА ОБЧИСЛЮВАЛЬНОЇ ТЕХНІКИ ТА ПРОГРАМУВАННЯ

Лабораторна робота №2

з курсу "Інтелектуальні комп’ютерні системи"

за темою: " Подання зображень в n-мірному векторному просторі "

                                                                               Виконала:

ст групи КІТ -14б

Богачов О. С.

Харків 2009

Мета: придбання й закріплення знань і одержання практичних навичок роботи з найпростішими алгоритмами розпізнавання на основі подання зображень у вигляді крапок в  n-мірному векторному просторі.

Індивідуальне завдання:

1. Розробити алгоритм і програму, що моделює розпізнавання різних об'єктів в n-мірному векторному просторі за допомогою відстаней (2)   (10).

2. Задатися розмірністю n-мірного векторного простору й числом m еталонних об'єктів образів (n  і  m  повинні бути не менш 5). Задайтеся декількома об'єктами й за допомогою виражень (2)   (8) визначити їхню приналежність до того або іншого образа.

3. Запропонувати свої приклади, що ілюструють недоліки відстаней (2)   (4) у порівнянні з відстанями (5)   (7).

4. Запропонувати не менш трьох своїх прикладів розпізнавання за допомогою відстані по Кендалу. Принаймні   в одному із прикладів відстань по Кендалу повинне приймати мінімальне значення, а в іншому   максимальне.

5. Запропонувати кілька прикладів розпізнавання за допомогою відстані по Чебышеву. В одному із прикладів відстань по Чебышеву повинне приймати значення, рівне Вашому номеру за списком у журналі групи.

6. Запропонуватие приклад розпізнавання, у якому величини відстаней по Чебишеву й Кендалу будуть рівні.

Хід роботи:

Еталонні зображення  X1, X2, ..., Xm деякого числа m  різних класів зображень або образів в n-мірному просторі задаються у вигляді крапок  (x11, x12, ..., x1n), (x21, x22, ..., x2n), ..., (xm1, xm2, ..., xmn). Будь-яке вхідне зображення Sі також представляється у вигляді крапки (xSі1, xSі2, ..., xSіn) у цьому просторі. Приналежність вхідного зображення Sk до одному з m  класів визначається за допомогою відстаней між крапкою Sі  й всіма крапками X1, X2, ..., Xm, що відповідають еталонним образам. Відстань і є мірою подібності вхідного зображення з еталонами класів або образів. Вхідне зображення ставиться до того образа, відстань до еталонного зображення якого мінімально, тобто вирішальним правилом є наступне співвідношення

При розпізнавання образів у даній лабораторній роботі використаються відстані по Евкліду: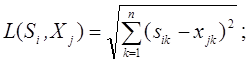

Також сума модулів разностей між відповідними компонентами  n-мірних векторів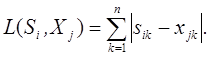

Особливий інтерес представляють відстані, у яких закладена ідея вирівнювання ваг доданків від різних компонентів, якщо вони істотно відрізняються по своїх абсолютних значеннях. Розглянемо відстань по Камберру: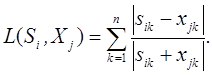

На рисунку 1 приведений розрахунок відстаней по Евкліду, по Камберру та за сумою модулів різностей між відповідними компонентами. За трьома формулами отримали розрахунок, у результаті якого видно, що вхідне зображення повністю подібне еталону 1, бо відстань дорівнює 0.

Рисунок 1.

При введенні розпізнавального символу. Неточному до еталонів. Ми отримаємо у результаті те, що показано на рисунку 2. Мінімальна відстані за усіма формулами належить еталону 1. Це мінімальна відстань, але не нульова, тому не можна сказати, що вхідне зображення повністю подібне до будь-якого еталону.

Рисунок 2.

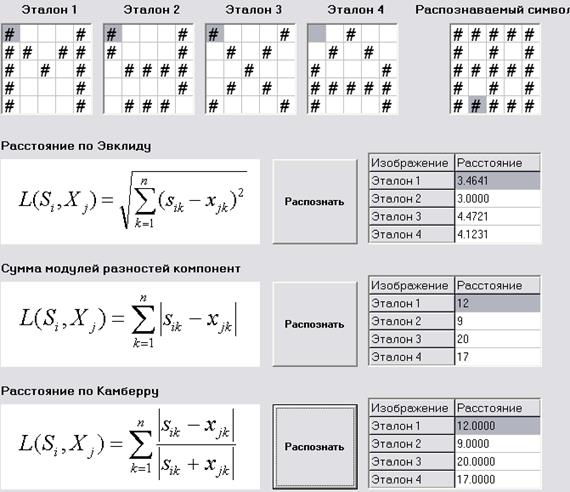
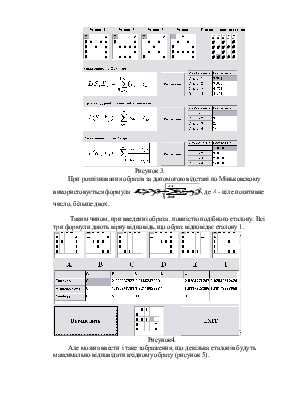
                                                Рисунок 3.

         При розпізнавання образів за допомогою відстані по Міньковскому використовується формула 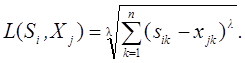, де - ціле позитивне число, більше двох.

          Таким чином, при введенні образа . повністю подібного еталону. Всі три формули дають вірну відповідь, що образ відповідає еталону 1.

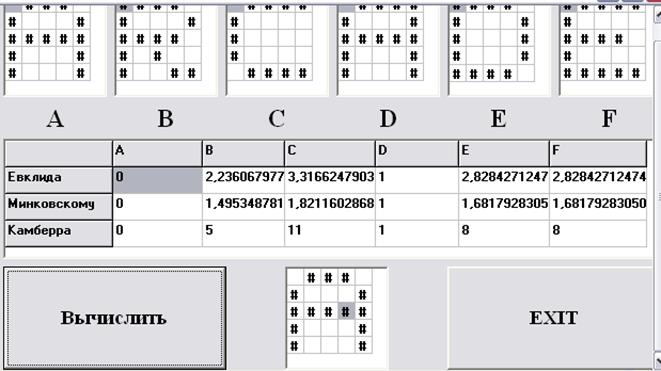
                                                       Рисунок4.

         Але можна ввести і таке зображення, що декілька еталонів будуть максимально відповідати вхідному образу (рисунок 5).

Рисунок 5.

Висновки: в результаті лабораторної роботи були придбані й закріплені знання і одержані практичні навички роботи з найпростішими алгоритмами розпізнавання на основі подання зображень у вигляді точок в  n-мірному векторному просторі.