Метод наискорейшего спуска решения задач нелинейного программирования
1. Теоретическая часть
Метод наискорейшего спуска (МНС) относится к поисковым методам решения задач нелинейного программирования, позволяющим получить приближенное решение с некоторой заданной точностью. Достоинством данного метода является то, что среди других поисковых методов он обеспечивает наименьшее число шагов решения задачи поиска.
В основе поисковых методов решения задач математического программирования лежит следующая идея.
Рассмотрим функцию ![]() двух
переменных
двух
переменных ![]() и
и ![]() (рис.1).
Проекция линии пересечения функции
(рис.1).
Проекция линии пересечения функции ![]() с плоскостью
с плоскостью ![]() , где F – некоторое
заданное значение функции
, где F – некоторое
заданное значение функции ![]() , на плоскости
, на плоскости ![]() называется линией постоянного уровня.
Задавая различные значения
называется линией постоянного уровня.
Задавая различные значения ![]() , можно получить другие
линии постоянного уровня и представить функцию
, можно получить другие
линии постоянного уровня и представить функцию ![]() совокупностью
этих линий (рис.2). Перемещение по поверхности, отображающей функцию
совокупностью
этих линий (рис.2). Перемещение по поверхности, отображающей функцию ![]() , из точки
, из точки ![]() в точку
в точку
![]() (рис.1) эквивалентно перемещению из точки
(рис.1) эквивалентно перемещению из точки ![]() в точку
в точку ![]() на
плоскости
на
плоскости ![]() (рис.2). Если это перемещение осуществлять
в направлении убывания функции
(рис.2). Если это перемещение осуществлять
в направлении убывания функции ![]() , то через определённое
число шагов(итераций) можно достигнуть окрестности точки локального минимума.
, то через определённое
число шагов(итераций) можно достигнуть окрестности точки локального минимума.
Если ![]() и
и ![]() - начальная и конечная точки перемещения на
К - ом шаге, то справедливо соотношение
- начальная и конечная точки перемещения на
К - ом шаге, то справедливо соотношение
![]() ,
(1)
,
(1)
где ![]() - вектор антиградиента,
задающий направление наибольшего убывания функции, а
- вектор антиградиента,
задающий направление наибольшего убывания функции, а ![]() -
величина шага перемещения.
-
величина шага перемещения.
Учитывая, что 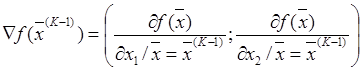 ,
(2)
,
(2)
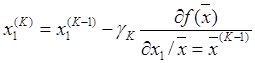 ,
(3)
,
(3)
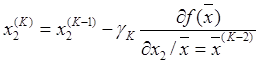 (4)
(4)
где правые сомножители второго слагаемого правой части
означают, что частные производные функции ![]() вычисляются
в точке
вычисляются
в точке ![]() .
.
Если из точки ![]() поиск
ведётся в направлении антиградиента -
поиск
ведётся в направлении антиградиента - ![]() , то в
точке
, то в
точке ![]() , являющейся начальной точкой следующего
шага, направление поиска будет определяться антиградиентом -
, являющейся начальной точкой следующего
шага, направление поиска будет определяться антиградиентом - ![]() . Векторы
. Векторы ![]() и
и ![]() в точке
в точке ![]() (рис.3),
перпендикулярны, откуда следует, что их скалярное произведение в данной точке
равно 0, т.е.
(рис.3),
перпендикулярны, откуда следует, что их скалярное произведение в данной точке
равно 0, т.е.
![]()
(5)
или ![]()
С учётом (2) выражение (5) примет вид:
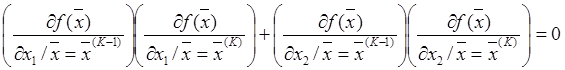 (6)
(6)
Решение уравнения (6) совместно с (3),(4) позволяет
определить величину ![]() на k – ом
шаге поиска по методу наискорейшего спуска. Процесс поиска минимума в
соответствии с (3) и (4) будет продолжаться до тех пор, пока не будет выполнено
условие:
на k – ом
шаге поиска по методу наискорейшего спуска. Процесс поиска минимума в
соответствии с (3) и (4) будет продолжаться до тех пор, пока не будет выполнено
условие:
![]() (7)
(7)
где ![]() - требуемая точность
определения минимума функции
- требуемая точность
определения минимума функции ![]() . Величина
. Величина ![]() задаёт размеры окрестности точки минимума,
удовлетворяющие заданной точности. С учётом (2) выражение (7) примет вид:
задаёт размеры окрестности точки минимума,
удовлетворяющие заданной точности. С учётом (2) выражение (7) примет вид:
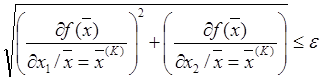 (8)
(8)
Таким образом, выражения (3), (4), (6), (8) являются основными рабочими соотношениями решения задач нелинейного программирования методом наискорейшего спуска.
2. Практическая часть.
1. Постановка задачи.
Бортовая ЭВМ осуществляет
расчёт координат точки посадки космического корабля. В начальный момент времени
корабль находится над точкой с условными координатами ![]() =
=![]() . Расход горючего зависит от местоположения
точки посадки и определяется отношением
. Расход горючего зависит от местоположения
точки посадки и определяется отношением ![]() , вид
которого задан в таблице вариантов исходных данных, где
, вид
которого задан в таблице вариантов исходных данных, где ![]() -
условные координаты точки посадки. Система управления корабля может обеспечить
отклонение от расчётной точки посадки не менее
-
условные координаты точки посадки. Система управления корабля может обеспечить
отклонение от расчётной точки посадки не менее ![]() .
.
Необходимо найти условные
координаты точки ![]() =
=![]() , при
посадке в которой расход горючего был бы минимальным.
, при
посадке в которой расход горючего был бы минимальным.
Решение типового примера.
Пусть x0 = (6;8), f(x) = x12 + 2 x22 - 2 x1 - 8 x2 + 12; e = 0.6.
Найдем
в первую очередь частные производные целевой функции ![]() :
:
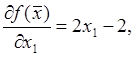
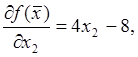
В соответствии с формулами (2),(3) координаты точки на k-ом шаге поиска рассчитываются следующим образом:
x1(k) = x1(k-1)-gk(2 x1(k-1)-2), (9)
x2(k) = x2(k-1)- gk(4 x2(k-1)-8), (10)
Для определения величины шага gk используем уравнение (6), которое в данном случае имеет вид:
(2 x1(k-1) - 2)(2 x1(k) - 2) + (4 x2(k-1) - 8)(4 x2(k) - 8) = 0. (11)
Поисковая процедура завершается при выполнении согласно (8) условия
![]() (12)
(12)
Последовательность поиска оптимального решения в соответствии (9)-(12) имеет вид:
Поскольку
начальной точкой поиска является ![]() = (6;8), то координаты
точки в конце 1-го шага (k=1) определяются в соответствии с (9)-(12) следующими
образом:
= (6;8), то координаты
точки в конце 1-го шага (k=1) определяются в соответствии с (9)-(12) следующими
образом:
x1(1) = x1(0)
- g1(2 x1(0)
- 2),
x2(1) = x2(0) - g1(4 x2(0)
- 8).
Тогда
x1(1) = 6 - g1(2*6 - 2) = 6 - g1*10,
x2(1) = 8 - g1(4*8 - 8) = 8 - g1*24.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.