Линейная оптимизация
Задача линейной оптимизации характеризуется тем, что целевая функция L(![]() ) и ограничения в виде равенств и/или неравенств
) и ограничения в виде равенств и/или неравенств ![]() (
(![]() = (x1,…,xn) – вектор переменных) – линейные. При этом в своей
исходной постановке задача линейной оптимизации может характеризоваться тем,
что требуется отыскать либо минимум, либо максимум целевой функции, а в
качестве ограничений могут выступать линейные равенства и неравенства
одновременно.
= (x1,…,xn) – вектор переменных) – линейные. При этом в своей
исходной постановке задача линейной оптимизации может характеризоваться тем,
что требуется отыскать либо минимум, либо максимум целевой функции, а в
качестве ограничений могут выступать линейные равенства и неравенства
одновременно.
Примером задачи линейной оптимизации является так называемая задача о
ресурсах (об использовании сырья): предприятия изготавливают n
видов продукции с использованием m видов сырья. Запасы сырья ограничены
и составляют bi единиц (i = ![]() ). Количество сырья, необходимое для изготовления
единицы продукции каждого вида, задаётся матрицей А =
). Количество сырья, необходимое для изготовления
единицы продукции каждого вида, задаётся матрицей А = ![]() (i =
(i = ![]() ; j =
; j = ![]() ). Доход, получаемый предприятием от реализации одной
единицы продукции каждого вида, равен cj.
Необходимо составить такой план выпуска продукции n видов
(т.е. сколько и чего производить), чтобы доход предприятия от её реализации был
максимальным.
). Доход, получаемый предприятием от реализации одной
единицы продукции каждого вида, равен cj.
Необходимо составить такой план выпуска продукции n видов
(т.е. сколько и чего производить), чтобы доход предприятия от её реализации был
максимальным.
В этом случае формальная постановка задачи оптимизации выглядит следующим образом. Если xj – число единиц продукции j-го вида, то, очевидно, что на их производство не может быть потрачено больше, чем bi единиц сырья i-го вида. Поэтому ограничения примут вид
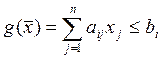 (
(![]() ),
),
т.е. имеем систему из m линейных неравенств, а целевая функция равна
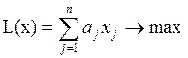 .
.
Другим примером задачи линейной оптимизации является задача о перевозках (см. лекцию «Постановка задачи оптимизации»). В этом случае, как можно заметить, в отличие от задачи о ресурсах, в качестве ограничений выступают линейные уравнения, а также требуется отыскать минимум целевой функции.
Обобщённый алгоритм решения задачи линейной оптимизации (линейного программирования) с помощью симплекс-метода состоит в следующем.
На первом шаге задача линейного программирования к канонической форме, которая характеризуется тем, что, во-первых, ограничения имеют вид линейных уравнений. Если в исходной постановке задачи оптимизации присутствуют ограничения-неравенства, то переход от ограничений-неравенств к ограничениям-уравнениям можно осуществить по следующим правилам.
Так, если в системе ограничений присутствует неравенство, у которого левая часть меньше правой, т.е. неравенство вида
ai1x1 + ai2x2 + … + aijxj +… + ainxn ≤ bi,
то к его левой части необходимо прибавить неотрицательную величину xn+i. В таком случае данное неравенство преобразуется в уравнение
ai1x1 + ai2x2 + … + aijxj +… + ainxn + xn+i = bi.
Аналогично, если в системе ограничений присутствует неравенство, у которого левая часть больше правой, т.е. неравенство вида
ai1x1 + ai2x2 + … + aijxj +… + ainxn ≥ bi,
то из его левой части необходимо вычесть неотрицательную величину xn+i . В таком случае данное неравенство преобразуется в уравнение
ai1x1 + ai2x2 + … + aijxj +… + ainxn – xn+i = bi.
Во-вторых, целевая функция должна быть устремлена к минимуму (иными словами, ищется минимум целевой функции). Если в исходной постановке задачи оптими-зации предусматривается отыскание максимума целевой функции, то для отыскания её минимума необходимо умножить целевую функцию на –1.
Тогда задачу линейного программирования в канонической форме можно сформулировать так: найти такие неотрицательные значения переменных x1, x2, …, xn, которые удовлетворяют ограничениям
a11x1 + a12x2 + … + a1jxj +… + a1nxn = b1;
a21x1 + a22x2 + … + a2jxj + … + a2nxn = b2;
…………………………………………
aj1x1 + aj2x2 + … + aijxj + … + ainxn = bi;
…. ……………………………………. (1)
am1x1 + am2x2 + … + amjxj + … + amnxn = bm
и обращают в минимум целевую функцию
L(![]() ) = c1x1 + c2x2 + … + cjxj + … + cnxn. (2)
) = c1x1 + c2x2 + … + cjxj + … + cnxn. (2)
При этом коэффициенты aij в системе ограничений и коэффициенты cj целевой функции могут принимать как положительные, так и отрицательные значения.
В такой постановке задача линейной оптимизации называется основной задачей линейного программирования (ОЗЛП).
Следует отметить, что при m = n данная задача имеет единственное решение и с точки зрения выбора решения не имеет смысла (т.е. по сути, не является оптимизационной). При m < n задача имеет множество решений и, следовательно, существует возможность выбора наилучшего (оптимального) решения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.