Динамическое программирование. Метод построения алгоритмов решения оптимизационных задач

Лекция 6: Динамическое программирование

0  Введение

В этой лекции вкратце изложен один из методов построения алгоритмов решения оптимизационных задач.

1  Метод

Динамическое программирование обычно применяется к задачам, в которых искомый ответ состоит из частей, каждый из которых в свою очередь дает оптимальное решение некоторой подзадачи. Динамическое программирование полезно, если на разных путях многократно встречаются одни и те же подзадачи; основной технический прием – запоминать решения встречающихся подзадач на случай, если та же подзадача встретится вновь.

Чтобы понять динамическое программирование, надо решать задачи. Но прежде рассмотрим пример.

2  Перемножение нескольких матриц

2.1  Задача

Пусть надо вычислить произведение n матриц:

A₁A₂…A_n

Необходимо найти такою расстановку скобок, чтобы стоимость вычисления (количество выполненных операций) была наименьшей.

2.2  Пояснения

Операция умножения матриц ассоциативна, потому скобки не влияют на результат. Но скобки могут повлиять на стоимость. Поясним.

Для того, чтобы умножить матрицу A размера p×q на матрицу B размера q×r, необходимо выполнить pqr операций умножения. При этом получается матрица размера p×r.

Вычисление произведения A₁A₂A₃ трех матриц можно выполнить двумя способами: (A₁A₂)A₃ и A₁(A₂A₃). Пусть размер матрицы A₁ – 10×100, A₂ – 100×5, A₃ – 5×50. Тогда в первом случае будет выполнено (10×100×5 + 10×5×50)=7500 операций умножения, во втором случае будет выполнено (100×5×50 + 10×100×50)=75000 операций.

2.3  Анализ и решение

Можно составить алгоритм, строящий все возможные расстановки скобок, который затем выбирает лучшую расстановку. Посмотрим, сколько существует таких расстановок.

Обозначим количество расстановок скобок в выражении из n матриц через P(n). Последнее умножение может быть между k-й и (k+1)-й матрицами. До этого мы вычислили отдельно произведения k и (n-k) матриц. Таким образом,

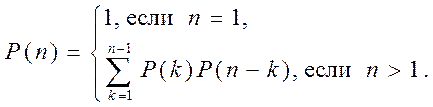
Если получить не рекуррентный вид формулы для P(n), то будет видно, что число расстановок экспоненциально зависит от n. Такой алгоритм не позволит решить поставленную задачу в реальных условиях.

Попробуем решить задачу при помощи динамического программирования.

Расстановка скобок разрывает произведение на две части. Стоимость (количество операций умножения) вычисления исходного произведения будет равна сумме стоимостей вычисления первой части, второй части и перемножения результатов. Чем меньше будет стоимость вычисления частей, тем меньше будет общая стоимость. Следовательно, оптимальное решение задачи о перемножении матриц содержит оптимальные решения задач о перемножении ее частей. Более того, задачи о перемножении частей могут пересекаться. Например, при вычислении произведения четырех матриц A₁A₂A₃A₄, возможны такие два разбиения: (A₁(A₂A₃))A₄ и A₁((A₂A₃)A₄). Оба разбиения включают произведение (A₂A₃).

Чтобы решить задачу, необходимо разбить исходное произведение на две части всевозможными способами (таких способов n-1), вычислить стоимости вычисления частей и выбрать лучшее разбиение. Если какая-то часть встретится повторно, необходимо воспользоваться уже вычисленным результатом. Запишем формально.

Обозначим через m[i, j] минимальное количество умножений, необходимое для вычисления произведения части произведения A_i…A_j. В частности, стоимость вычисления всего произведения равна m[1, n]. Размер матрицы A_i равен p_i-1×p_i. Согласно нашим рассуждениям,

3  Задания и задачи

3.1  Задание

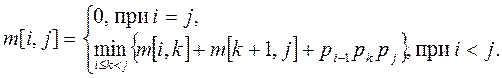
Реализуйте алгоритм на языке программирования, изложенный в разделе 2.3.

3.2  Задачи

1.  Задача об оптимальной триангуляции

Задан выпуклый многоугольник. Необходимо разбить его диагоналями на треугольники так, чтобы общий периметр всех треугольников был наименьший. Составьте эффективный алгоритм, решающий задачу.

Указание. Сравните с задачей об оптимальном умножении матриц.

2.  3×n + 1

Рассмотрим такой алгоритм:

1.  Ввод n

2.  Печать n

3.  Если n=1, то конец

4.  Если n нечетное, то n ← З×n+1

5.  Иначе n ← n / 2

6.  Перейти на шаг 2

Если на вход алгоритма задать число 22, то будет напечатана роследовательность чисел: