Описание интерфейса программной части программно‑аппаратного комплекса «Моделирование многосвязной системы», страница 3

Итак, рассмотрим случай, когда идентифицируемая система полагается системой третьего порядка.

При подаче сигналов были получены следующие результаты:

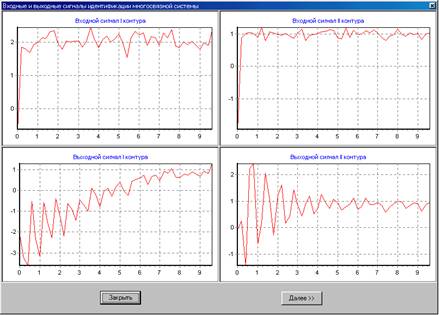
Рис. 4.12. Результаты подачи сигналов на входы: графики входных воздействий и полученные результаты на выходе.

Теперь, при нажатии кнопки «Далее», а затем кнопки закрыть, можно посмотреть коэффициенты полученных разностных уравнений.

Рис. 4.13. Первый вариант разностных уравнений для идентификации системой третьего порядка.

Для сверки моделируемой системы с реальной нажимаем кнопку «Проверить» и получаем следующие результаты.

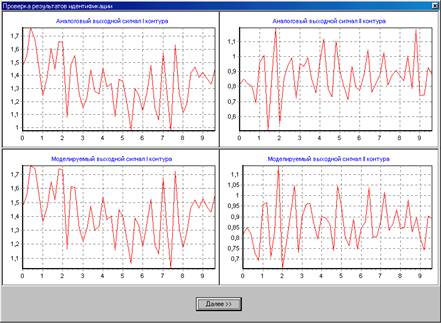
Рис. 4.14. Проверка для системы, идентифицируемой третьим порядком.

Результаты проверки можно считать удовлетворительными, но не более. Погрешность значительна, а временами очень значительна; что особенно характерно для второго контура системы.

Стоит провести эксперимент второй раз, при тех же условиях. Вновь подадим на систему сигналы и получаем результаты.

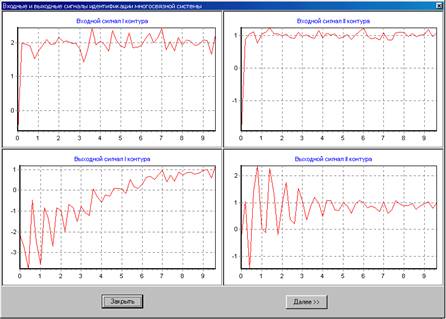
Рис. 4.15. Результаты подачи сигналов на входы: графики входных воздействий и полученные результаты на выходе.

Если сравнить рисунки 4.12 и 4.15, то можно заметить, что они похожи. Это неудивительно: система одна и испытания проводились при одних и тех же условиях. Также неудивительно и то, что они всё‑таки немного различаются: входные воздействия ведь случайны.

Рис. 4.16. Второй вариант разностных уравнений для идентификации системой третьего порядка.

При сравнении рисунков 4.13. и 4.16. выясняем, что результаты довольно сильно разнятся, причём для второго контура это проявляется более явно.

Далее необходимо проверить, насколько сильно отличаются результаты моделирования от реальных.

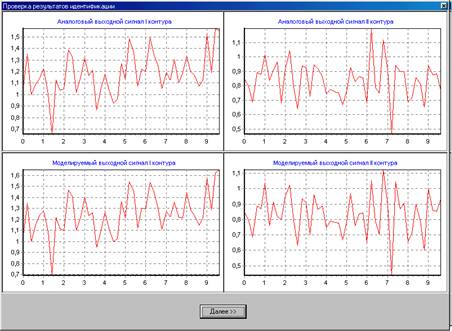
Рис. 4.17. Проверка смоделированной для третьего порядка системы для второй попытки идентификации.

В общем‑то, результат такой же, как и на рисунке 4.14.: погрешность значительна, особенно для второго контура, хотя смоделированные сигналы довольно похожи на реальные.

Чтобы уменьшить погрешность, попробуем увеличить порядок модели до седьмого. Остальные параметры идентификации оставим без изменения.

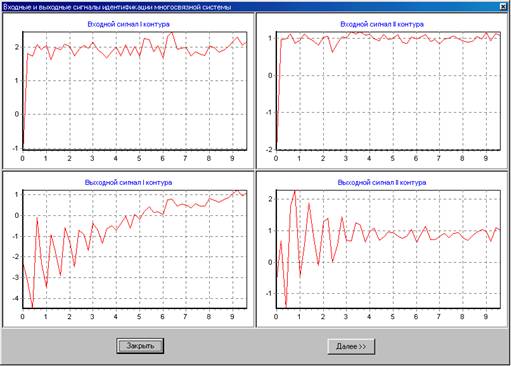
Рис. 4.18. Результаты подачи сигналов на систему.

Посмотрим коэффициенты разностных уравнений.

Рис. 4.18. Коэффициенты разностных уравнений для системы седьмого порядка; первая идентификация.

Проверка адекватности модели даёт следующие результаты.

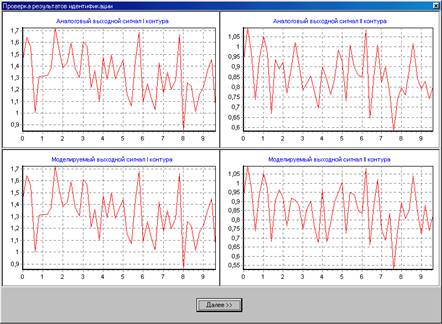
Рис. 4.19. Проверка первой попытки идентификации системой седьмого порядка.

Как видно из рисунка, результаты моделирования стали гораздо лучше: для первого контура они почти идеальны, а у второго хоть и выше погрешность, но тоже весьма неплохо.

Теперь попробуем повторить испытания.

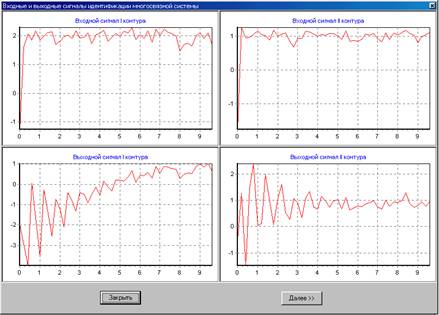
Рис. 4.20. Результаты подачи сигналов на систему.

Коэффициенты разностных уравнений будут иметь вид.

Рис. 4.21. Коэффициенты разностных уравнений для моделирования системой седьмого порядка; вторая попытка.

Сравнивая результаты с рис.4.18., приходим к выводу, что они сильно различаются.

Сравним данную модель с реальной системой.