Расчёт электрических цепей с индуктивно-связанными элементами: Методические указания к выполнению расчётно-графической работы № 2

Таблица 1   -   Базовые параметры элементов электрической цепи

Вариант	1	2	3	4	5	6
Em1, B	70.7	141,4	198	99	169	106
fe1, град.	60	-30	90	-45	0	135
Em3 , B	282,8	141,4	99	198	106	169
fe3 , град.	-30	120	0	90	45	-60
Em4 , B	70.7	141,4	99	198	106	169
fe4, град.	-120	90	-60	135	60	-45
R10, Ом	15	25	35	30	20	40
L10, мГн	95,5	79,6	111,4	31,8	86	105
C10, мкФ	199	91	79,6	63,7	106	187,2
R20, Ом	50	60	30	40	55	35
L20, мГн	105	51	31,8	95,5	63,6	127,3
C20, мкФ	91	187,2	106	159,2	79,6	212,2
R30, Ом	20	35	50	45	30	25
L30, мГн	63,7	79,6	95,5	44,6	127,3	95,5
C30, мкФ	212,2	127,3	91	159	318,3	144,7
R40, Ом	30	60	50	20	45	35
L40, мГн	44,6	127,3	105	86	31,8	111,4
C40, мкФ	106	127,3	199	187,2	91	318,3
L50, мГн	127,3	86	95,5	105	63,6	79,6
К1-2	0,40	0,50	0,35	0,45	0,30	0,55
К4-5	0,30	0,35	0,55	0,50	0,45	0,40

Таблица 2  -  Переводные коэффициенты для значений параметров         элементов цепи

№  цепи	кR	кL	кс	Отсутствуют            элементы             в схеме	Отсутствуют источники           ЭДС         в схеме
1	1,00	1,00	1,00	L2, C2, R4	E3, E4
2	1,10	1,10	0,90	C1, L2, R3	E1, E4
3	0,80	1,00	1,25	L2, R3, C4	E1, E3
4	1,15	0,95	1,30	C2, R3, L5	E3, E4
5	0,85	1,15	1,20	C2, R4, L5	E1, E4
6	1,10	1,20	1,15	C2, C4, L5	E1, E3
7	1,20	1,10	0,95	L2, R4, C4	E3, E4
8	1,25	0,90	1,10	L2,  C3,  С4	E1, E4
9	1,30	1,20	0,85	С1,  C2,  L2	E1, E3
10	1,15	1,20	1,00	C3, С4, L5	E3, E4
11	1,00	1,20	1,00	C2, С4, L5	E1, E4
12	1,20	1,00	1,20	C2, L5	E1, E3
13	0,80	1,00	1,10	L3, С4, L5	E3, E4
14	1,10	0,95	1,30	С1,  L2, C4	E1, E4
15	1,25	1,10	0,80	C1, L2, C4	E1, E3
16	0,90	1,30	0,90	C1, L2, R3	E3, E4
17	1,15	0,90	1,20	C2, L3, L5	E1, E4
18	1,25	1,15	1,10	R1 , L2,  С4	E1, E3
19	1,10	1,10	1,20	L2, C3, R4, C4	E3, E4
20	1,30	1,20	0,90	L2, R4, C4	E1, E4
21	0,90	1,25	1,15	C2, R3, L5	E1, E3
22	1,10	1,10	1,10	L3, C3, L5	E3, E4
23	0,90	0,90	0,90	C3, R4, С4, L5	E1, E4
24	1,10	1,25	1,15	L2, L3, C4	E1, E3
25	1,20	1,15	1,20	C1, L3, R4, L5	E3, E4
26	1,30	1,20	1,10	L2, C2, R3	E1, E4
27	1,25	1,10	1,20	C3, R4, L5	E1, E3
28	1,00	1,20	0,95	L2,   R3, С4	E3, E4
29	1,30	1,30	1,00	C2, L3, L5	E1, E4
30	1,20	1,20	1,20	L2, L3, С4	E1, E3
31	1,15	1,15	1,30	L2,   С3, R4	E1, E3
32	1,35	1,25	1,15	C1, R4, L5	E1, E4

Методические указания к решению задачи

Четырёхполюсник является передаточным звеном между    источником энергии и нагрузкой. Таким образом, для заданной цепи входом пассивного четырёхполюсника будут зажимы источника ЭДС, а выходом четырёхполюсника – зажимы переменного сопротивления R₂, помеченного на схеме стрелкой (рисунок 2):

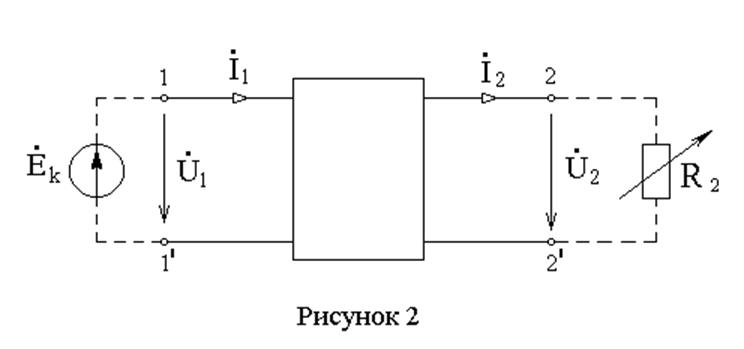
Уравнение четырёхполюсника в А-форме записывается следующим образом:

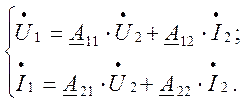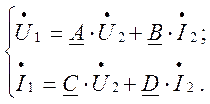         или                         ( 1 )

Здесь: ,  ,  ,    - коэффициенты        четырёхполюсника, связанные соотношением  .

При обратном включении четырёхполюсника (при перемене направления передачи энергии: от зажимов  2-2^/  к зажимам  1-1^/ ) уравнение четырёхполюсника в А-форме записывается:

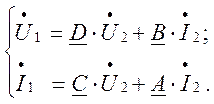                                                                                       ( 2 )

Комплексные сопротивления индуктивностей и ёмкостей     синусоидальному току заданной частоты определятся по формулам:

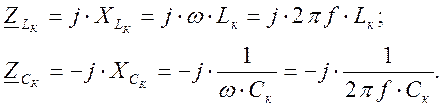                                         ( 3 )

Сопротивление взаимной индукции определится по заданному коэффициенту индуктивной связи соответствующих индуктивно-связанных элементов цепи и их параметрам:

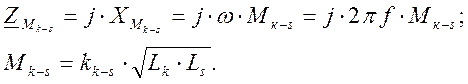                                      ( 4 )

При вычерчивании заданной расчётной схемы индивидуального варианта исключаем отсутствующие элементы и источники энергии, а также учитываем магнитную связь между соответствующими элементами при взаимной индуктивности М_ks путём разметки одноимённых зажимов. Одноимённые зажимы на схеме помечаются значками (·  или  *). Зажимы двух индуктивно-связанных катушек называют одноимёнными, если при одинаковом направлении токов относительно этих зажимов потокосцепления самоиндукции и     взаимной индукции в каждой катушке действуют согласно (суммируются). Одноимённость зажимов зависит от направления намотки витков катушек и от их взаимного расположения.

Комплексные сопротивление ветвей схемы (без учёта         индуктивной связи элементов и сопротивления нагрузки R_нагр. = R₂)   определятся:

             ;

             ;

             ;

             .

Комплексное действующее значение ЭДС (напряжения на входе   четырёхполюсника   ) определится:

 

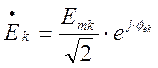                                     .                                       ( 5 )

Расчёт электрических цепей, содержащих индуктивно-связанные элементы возможен на основании применения законов Кирхгофа или методом контурных токов.

Заданная цепь имеет два узла (у = 2) и четыре ветви (в = 4). Тогда по законам Кирхгофа для цепи должно быть составлено      четыре уравнения [одно по первому закону Кирхгофа для одного из двух узлов цепи (у – 1 = 1) и три уравнения по второму закону   Кирхгофа для независимых контуров цепи (в – у + 1 = 3)]. По методу  контурных токов должно быть составлено три уравнения для       контурных токов (как и по второму закону Кирхгофа): .   Контуры целесообразно выбирать таким образом, чтобы ветвь с   источником ЭДС входила только в один контур.

При составлении уравнений по второму закону Кирхгофа      (и методу контурных токов) к напряжению на индуктивном элементе в ветви “k” 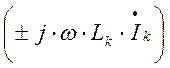  необходимо добавить напряжение взаимной индукции от тока, действующего в ветви  “s” 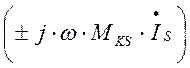    (если между этими ветвями есть индуктивная связь, т.е. M_ks ¹ 0). При этом  напряжение взаимной индукции имеет знак “плюс”, если направление обхода индуктивного элемента в ветви “k” и выбранное положительное направление тока в индуктивно-связанном элементе ветви “s” 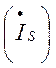 совпадают относительно одноимённых зажимов этих  элементов.

Для нахождения коэффициентов четырёхполюсника записанная система четырёх (по законам Кирхгофа) или трёх (по методу контурных токов) уравнений должны быть сведена соответствующими подстановками к системе двух уравнений, исключая промежуточные для четырёхполюсника переменные, оставляя только ток      источника   и ток нагрузки    , вводя обозначения:

                               ,   .                                  ( 6 )

Из сравнения полученных уравнений с уравнением четырёхполюсника в А-форме записи ( 1 ) найдутся коэффициенты заданного четырёхполюсника.

Подставляя в уравнение четырёхполюсника в А-форме заданные параметры цепи (   и   ) и найденные значения коэффициентов четырёхполюсника, можно найти токи   и .

К.п.д.  четырёхполюсника найдётся по формуле:

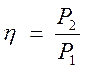                                   ,                                                  ( 7 )

где   ;        .

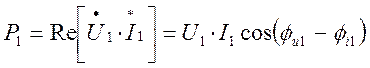На основании найденных коэффициентов четырёхполюсника может быть  построена  Т – образная  или   П – образная  схемы  замещения (рисунок 3). Под физически реализуемой схемой замещения понимается такая схема, в которой параметры элементов   R, L, C   положительны.

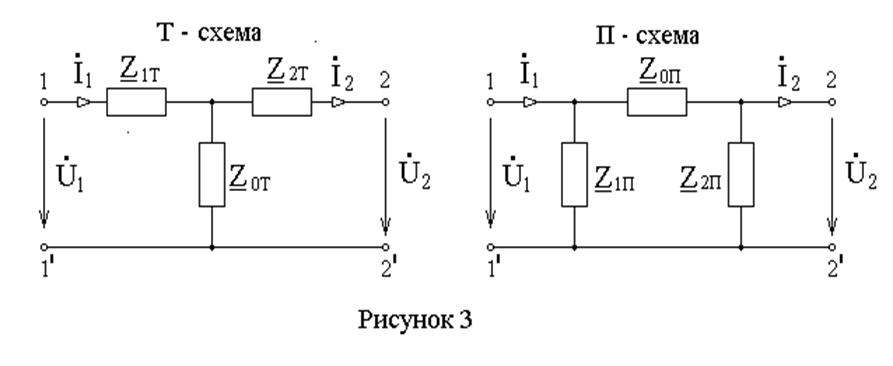
Для заданного четырёхполюсника параметры элементов     эквивалентных схем замещения по найденным коэффициентам  определятся по формулам:

для Т – схемы замещения

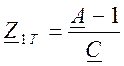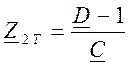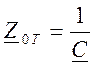                  ,    ,    ;                        ( 8 )

для П – схемы замещения

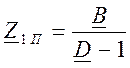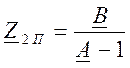                  ,    ,    .                        ( 9 )

Пример расчёта

Исходные данные индивидуального варианта:

№ цепи	кR	кL	кс	Отсутствуют    элементы      в схеме	Отсутствуют источники       в схеме
0	1,00	1,20	1,20	L2,  R4,	E1,  E4

Em3, B	fe3, град	R10, Ом	L10, мГн	C10, мкФ	R20, Ом	C20, мкФ	R30, Ом	L30, мГн	C30, мкФ	L40, мГн	C40, мкФ	L50, мГн	K4-5
282,84	30	30	37,14	88,4	40	176,8	50	92,84	53,1	106,1	106,1	212,2	0,5

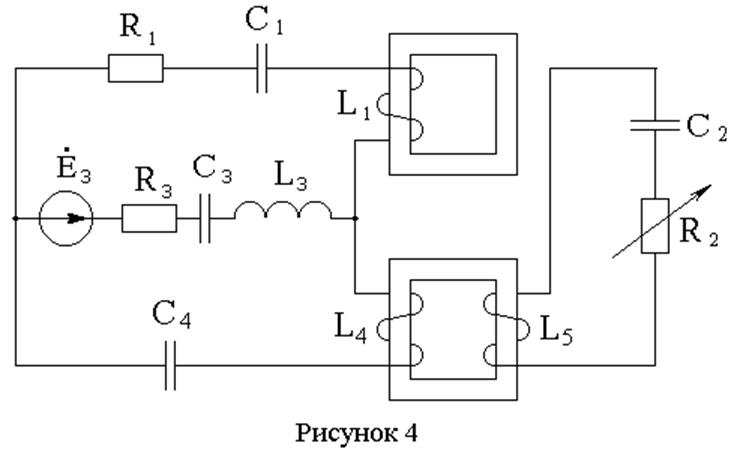
С учётом заданных условий схема электрической цепи имеет вид, показанный на рисунке 4:

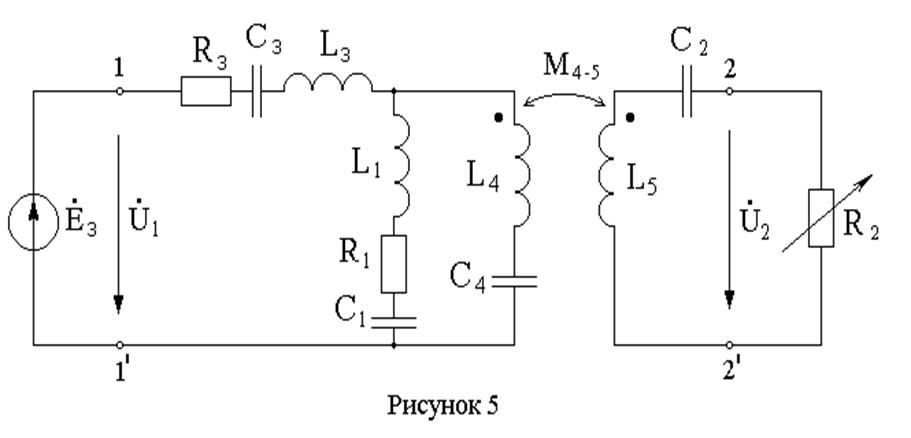
  Выделяя входные зажимы (зажимы источника ЭДС  Е₃) и выходные зажимы (зажимы переменного сопротивления R₂),         получим схему заданного четырёхполюсника:

         Сопротивления элементов цепи синусоидальному току        заданной частоты:

          Ом;    

          Ом;

          Ом;                                    

          Ом;

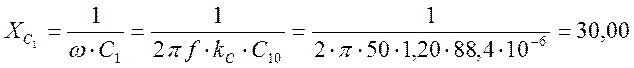          Ом;

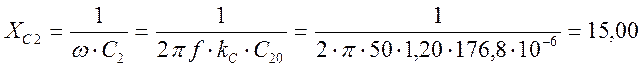          Ом;

          Ом;

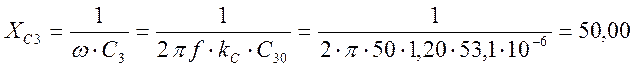          Ом;

          Ом;

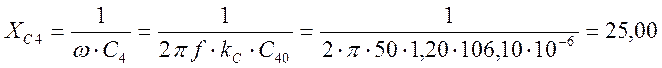          Ом;

          Ом.

Комплексные сопротивления ветвей цепи (рисунок 6):

        Ом;

        Ом;

        Ом;

        Ом.

Взаимная индуктивность индуктивно-связанных катушек:

мГн.

Комплексное сопротивление взаимной индуктивности:

        Ом.

Комплексное действующее значения  ЭДС  (напряжение на входе четырёхполюсника):

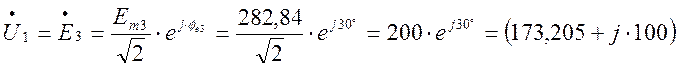В.

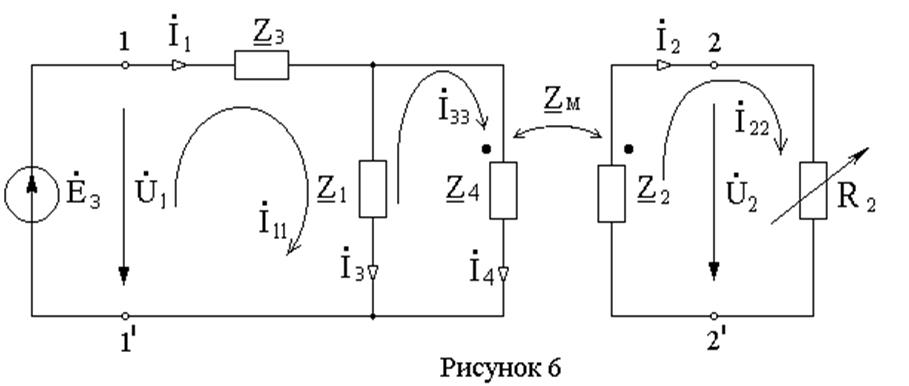
Заданная цепь имеет два узла (у = 2) и четыре ветви (в = 4). Таким образом для определения токов ветвей по законам Кирхгофа для цепи должно быть составлено четыре уравнения [одно по    первому закону Кирхгофа для одного из двух узлов цепи (у – 1 = 1) и три уравнения по второму закону Кирхгофа для независимых