




















Проверка правильности расчёта осуществляется на основании составления баланса мощностей (равенства активных и реактивных мощностей источника и приёмников):
![]() ;
; ![]() ;
;
![]() ;
;
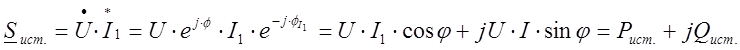 ;
;
![]() ;
; ![]() .
.
Здесь ![]() -
сопряжённый комплекс тока.
-
сопряжённый комплекс тока.
По найденным комплексным действующим значениям токов ветвей их законы изменения во времени (мгновенные значения) запишутся:
![]() ;
;
![]() ;
;
![]() .
.
Векторной диаграммой называют совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся величины одной частоты. Топографической диаграммой называют такую векторную диаграмму комплексных потенциалов (напряжений), когда каждой точке схемы соответствует определённая точка на векторной диаграмме. Топографическую диаграмму для электрической схемы строят, откладывая на комплексной плоскости векторы комплексных напряжений последовательно для всех элементов цепи, получая комплексные потенциалы всех точек схемы.
Алгоритм построения векторных диаграмм
1.Выбирают масштаб тока mi и в этом масштабе на комплексной плоскости из начала координат откладывают найденные комплексные действующие значения токов ветвей (построение векторов удобнее выполнять по их проекциям на координатные оси).
2.Обозначают все точки ветвей схемы (буквами или цифрами).
3.Определяют комплексные действующие значения напряжений на всех элементах цепи.
4.Потенциал одной из точек схемы принимают за нулевой и помещают эту точку в начало координат.
5.Выбирают масштаб напряжений (потенциалов) mu и в этом масштабе последовательно на комплексной плоскости строят комплексные потенциалы всех точек схемы.
При построении топографической диаграммы целесообразно выбирать последовательность построения такой, чтобы обход пассивных элементов схемы был против направления тока в них. В этом случае потенциалы следующих точек возрастают на величину падения напряжения на соответствующем элементе и на диаграмме вектора суммируются (в противном случае потенциал уменьшается и вектора необходимо вычитать).
Пример №1
Исходные данные варианта:
Um,B |
f, град |
R10, Ом |
L10, мГн |
C10,мкФ |
R20, Ом |
L20, мГн |
C20,мкФ |
R30, Ом |
L30, мГн |
C30,мкФ |
R40, Ом |
L40, мГн |
C40,мкФ |
212,13 |
-30 |
30 |
35,01 |
90,95 |
40 |
89,13 |
162,4 |
50 |
63,7 |
41,34 |
10 |
105 |
187,2 |
|
№ цепи |
кR |
кL |
кс |
Отсутствуют элементы в схеме рис.1 и рис.2 |
Отсутствуют источники в схеме рис.2 |
Определить в схеме рис.2 |
|
0 |
0,90 |
1,00 |
1,40 |
L3, L4, C4 |
e2 |
i4 |
Для рассматриваемого варианта схема цепи показана на рис.5.
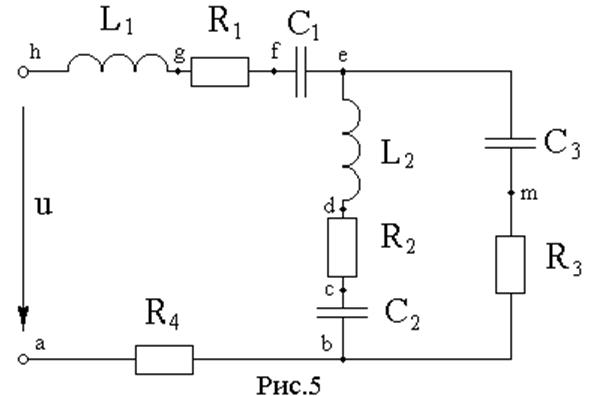
Сопротивления элементов цепи:
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
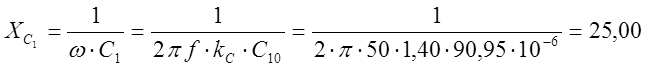 Ом;
Ом;
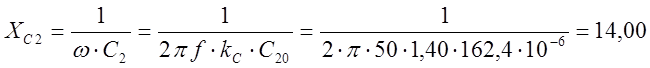 Ом;
Ом;
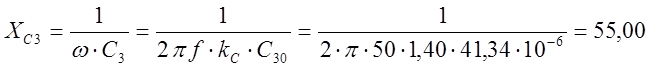 Ом.
Ом.
Комплексные сопротивления ветвей цепи (рис.3):
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом.
Ом.
Комплексное сопротивление параллельного участка цепи:
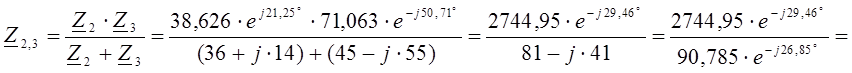
![]() Ом.
Ом.
Эквивалентное комплексное сопротивление всей цепи:
![]() Ом.
Ом.
Комплексное действующее значение приложенного напряжения:
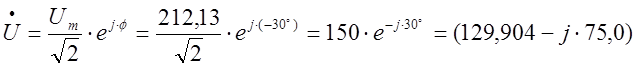 В.
В.
Комплексное действующее значение токов ветвей:
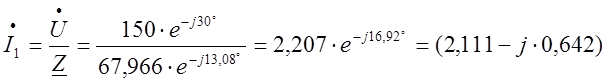 А;
А;
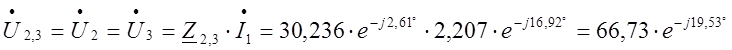 B.
B.
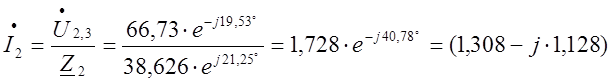 А;
А;
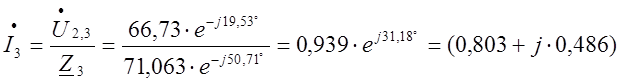 А.
А.
Баланс мощностей источника и приёмников:
![]() ;
; ![]() ;
;
![]() ;
;
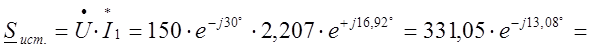 ;
;
![]() ВА;
ВА;
![]() Вт;
Вт; ![]() ВАр;
ВАр;
![]()
![]() Вт;
Вт;
![]()
![]() ВАр.
ВАр.
Погрешность расчёта:
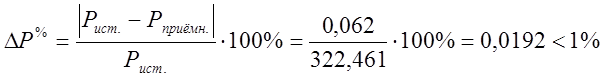 ;
;
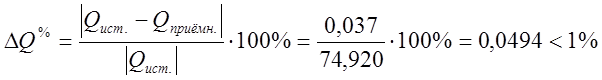 .
.
Баланс мощностей соблюдается, т.е. расчёт выполнен верно.
По найденным комплексным действующим значениям токов ветвей их законы изменения во времени запишутся:
![]() А;
А;
![]() А;
А;
![]() А.
А.
Для построения топографической диаграммы находим напряжения на всех элементах цепи:
![]() B;
B; 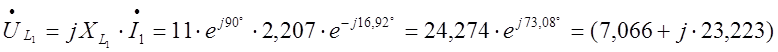 B;
B; 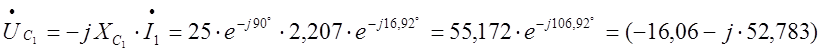 B;
B;
![]() B;
B; 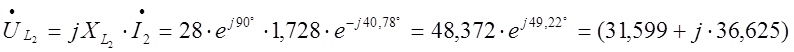 B;
B; 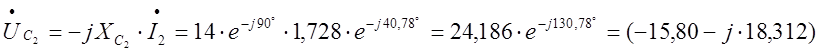 B;
B;
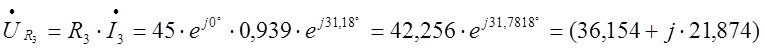 B;
B; 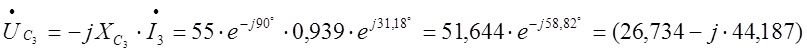 B;
B;
![]() B.
B.
За точку нулевого потенциала схемы примем точку “а”, т.е.
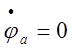 .
.
Тогда потенциалы остальных точек схемы определятся:
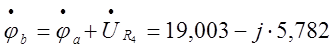 ;
;![]()
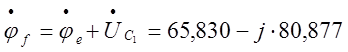 ;
;
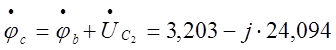 ;
;
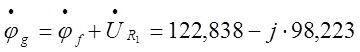 ;
;
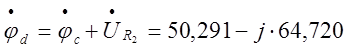 ;
;
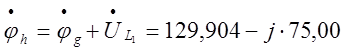 ;
;
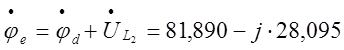 ;
;
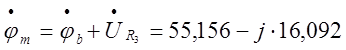 .
.
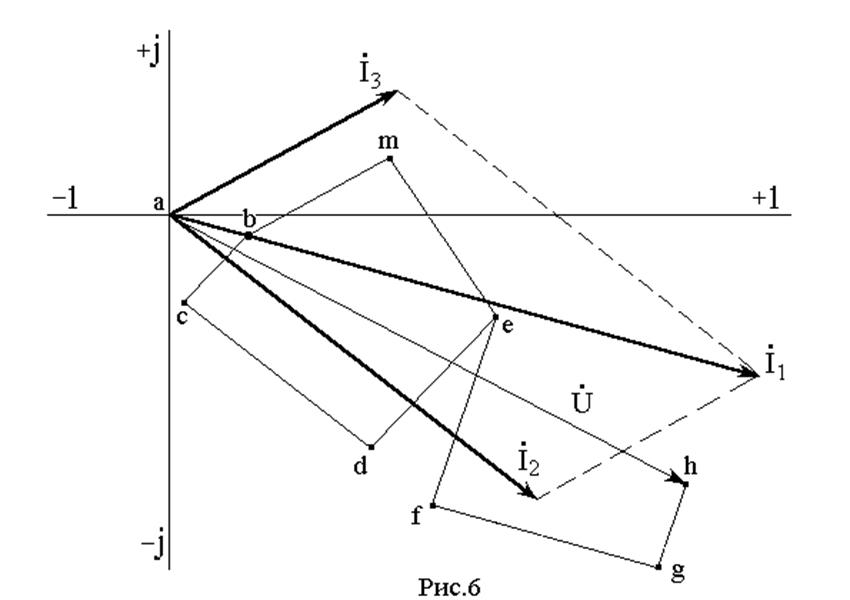
По найденным напряжениям на элементах цепи и потенциалам точек схемы строится топографическая диаграмма напряжений. Векторная диаграмма токов и топографическая диаграмма напряжений для заданной цепи показана на рис.6.
Методические указания к решению задачи №2.
Исходная цепь синусоидального тока содержит несколько источников энергии (один из них – источник тока). Цепь имеет три узла (у = 3) и пять ветвей (в = 5), причём одна из ветвей содержит источник тока (вит = 1).
Метод узловых напряжений (потенциалов) основан на применении первого закона Кирхгофа и закона Ома. По этому методу составляется (у – 1) уравнение для междуузловых напряжений, при условии, что один из узлов принимается за опорный. [ По методу узловых потенциалов опорный узел заземляется - его потенциал принимается равным нулю, и уравнения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.