Процесс управления технологической установкой. Представление исходной логической функции в виде СКНФ. Реализация устройства на базе мультиплексора

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Сибирский государственный индустриальный университет»

Кафедра АЭП и ПЭ

Курсовая работа

по дисциплине «Элементы систем автоматики и микропроцессорная техника»

Выполнил: студент гр. АЭП-042

                    Ручкин А.С.

Проверил:  доцент, к.т.н.

                     Яскевич М.М.

Новокузнецк, 2007

Задание на курсовую работу

Процесс управления некой технологической установкой описывается логической функцией f четырех переменных х₁, х₂, х₃, х₄. Требуется:

1.  Записать логическую функцию в виде СКНФ.

2.  Минимизировать эту логическую функцию одним из известных методов. Выбор метода обосновать.

3.  Составить наиболее простую схему реализации устройства в минимальном базисе И-НЕ. Начертить принципиальную схему устройства.

4.  Составить схему реализации устройства на базе мультиплексора. Начертить принципиальную схему.

5.  Составить схему релейно-контактного эквивалента логического устройства, поставив в соответствие логическому аргументу х_i замыкающий контакт, аргументу - размыкающий контакт, логической функции f – исполнительное устройство (например, обмотку реле).

Таблица 1 – Задание на курсовую работу

X1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
X2	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
X3	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
X4	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
F33	1	0	1	1	0	0	1	1	0	0	0	1	1	1	0	0

1. Представление исходной логической функции в виде СКНФ

          Запись логической функции в виде СДНФ или СКНФ позволяет упростить вид выражения и увеличить читаемость функции. В совершенной конъюнктивной нормальной форме (СКНФ) каждая входящая конъюнкта включает все переменные (с инверсиями и без них), что позволяет оценить сразу все логические члены.

          Опишем все конъюнкты, исходя из данной в задании таблицы истинности (их будет 8, так как в таблице истинности есть 8 ложных значений функции):

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

          Тогда СКНФ запишется:

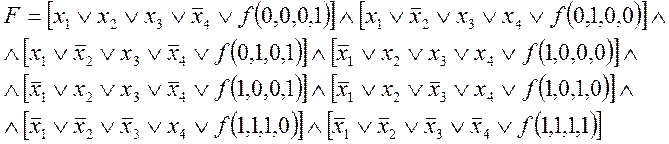
2. Минимизация СКНФ

          Минимизация логической функции необходима, так как позволяет избавиться от лишних логических действий в выражении и реализовать данную функцию наименьшим количеством элементов.

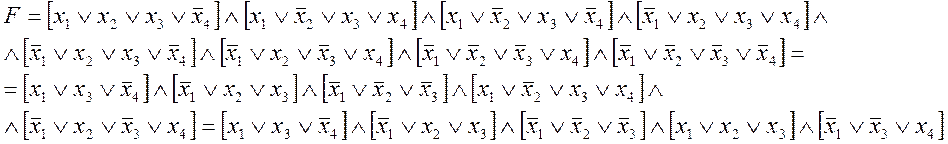
          Преобразуя данную логическую функцию, получаем минимальную конъюнктивную нормальную форму МКФ:

3. Переход в базис И–НЕ

          Записываем функцию в минимальной конъюнктивной нормальной форме (именно эту форму удобнее всего представлять в базисе И–НЕ или ИЛИ–НЕ так как требуется наименьшее количество элементов при одинаковом конечном результате).

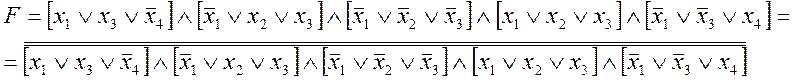
          Для того чтобы представить данную функцию в базисе И–НЕ необходимо произвести некоторые преобразования исходной МКНФ путём использования закона Де Моргана:

1);

2);

3);

4);

5)

          По полученным выражениям составляем схему представления исходной функции в базисе И–НЕ (она приведена на рисунке 1).

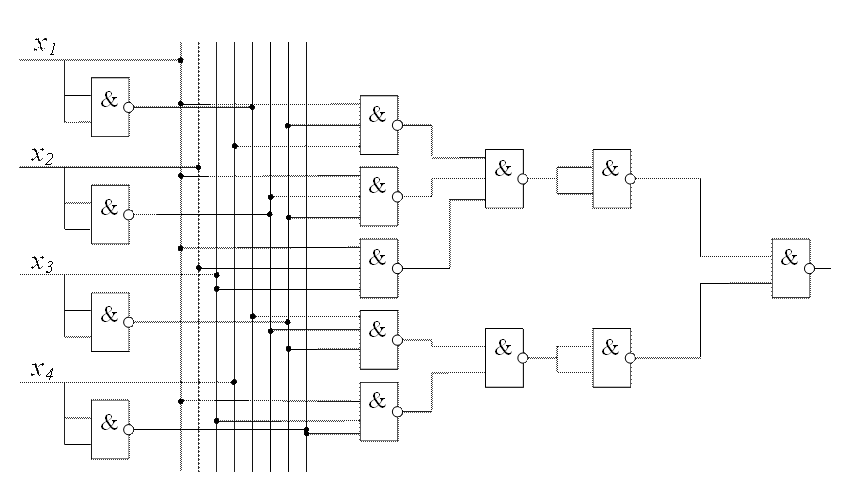
Рисунок 1 – Схема представления исходной функции в базисе И–НЕ

Для реализации данной схемы в минимальном базисе И-НЕ используем интегральные микросхемы К561ЛА8 (2И-НЕ).

4. Реализация устройства на базе мультиплексора

Мультиплексор является устройством, которое осуществляет выборку одного из нескольких входов и подключает его к своему выходу. Мультиплексор имеет несколько информационных входов (D0, D1,…), адресные входы (A0, A1,…), вход для подачи синхронизирующего сигнала С и один выход Q.

Каждому информационному входу мультиплексора присваивается номер, называемый адресом. При подаче синхронизирующего сигнала на вход С мультиплексор выбирает один из его входов, адрес которого задается двоичным кодом на адресных входах, и подключает его к выходу.

Запишем минимизированную функцию в конъюнктивной нормальной форме:

          По данной функции составим таблицу, в которой выходная функция мультиплексора ставится в соответствие со значениями на адресных входах (приведена в таблице 2).

Таблица 2 – Таблица соответствия адресных входов и значения функции

А­­­­0	А1	А2	Q
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0

          По данной таблице составляем выходную функцию мультиплексора:

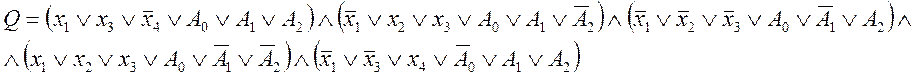
          По данной функции построим схему мультиплексора (рисунок 2):

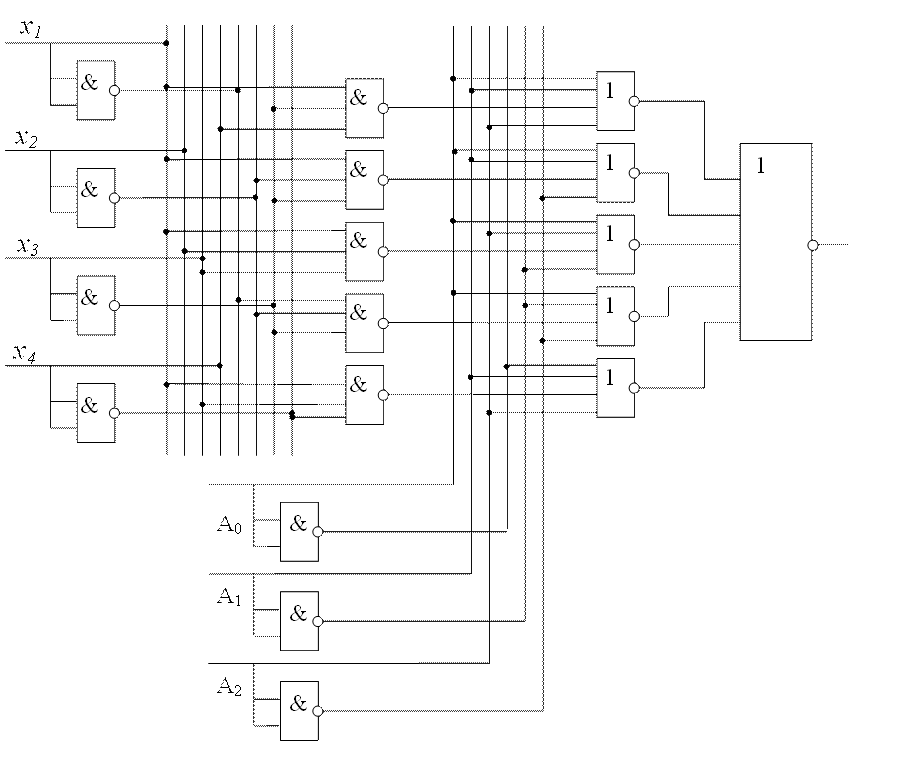
Рисунок 2 – Схема мультиплексора

5. Схема релейно-контакторного эквивалента
логического устройства

          Запишем исходную функцию в минимальной конъюнктивной нормальной форме:

          Исходя из задания, логические элементы представляем в виде замыкающих контактов, а контакты  – виде размыкающих контактов. Логическую функцию F представляем в виде обмотки реле. Из данных условий построим схему релейно-контакторного эквивалента логического устройства:

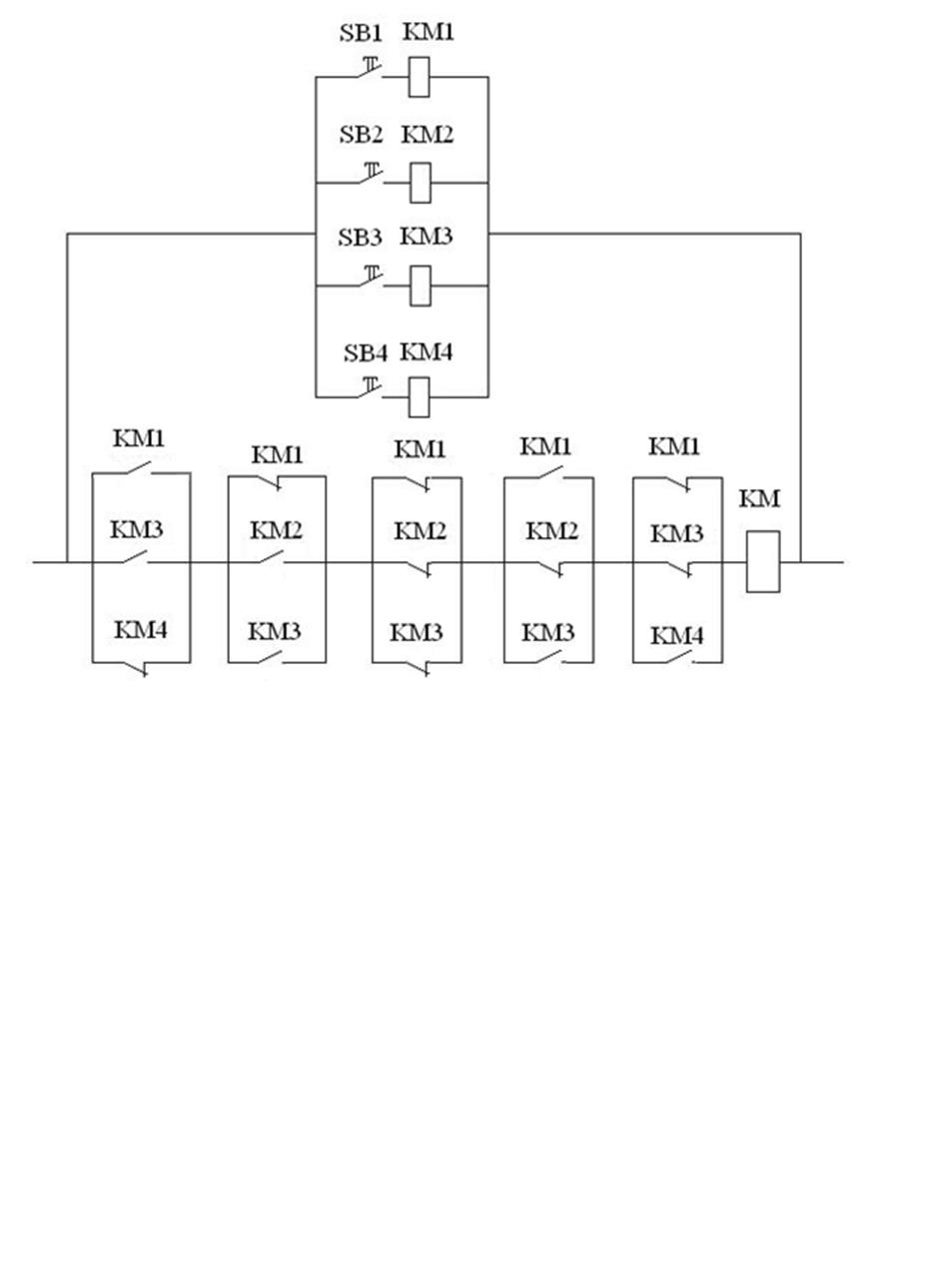
Рисунок 3 – Схема релейно-контакторного эквивалента
логического устройства

Список литературы

1.  Забродин Ю.С. Промышленная электроника: Учебник для вузов. – М.: Высш.школа, 1982. – 496 с.

2.  Калабеков Б.А. Цифровые устройства и микропроцессорные системы/ Б.А. Калабеков, И.А. Мамзелев.. – М.: Радио и связь, 1987.

3.  Элементы систем автоматики и микропроцессорная техника: Задания и методические указания к выполнению курсовой работы для студентов специальности 180400 «Электропривод и автоматика промышленных установок и технологических комплексов», обучающихся по очно-заочной, заочной и сокращенной образовательной программам: Метод.указ./Сост.: А.К.Мурышкин. – СибГИУ, Новокузнецк, 2003. – 8с.