Проектирование электропривода кранового электрооборудования

Приведение моментов, сил, жестокостей связи, моментов инерции к одной скорости.

Определим радиус приведения для поступательно-движущейся массы:

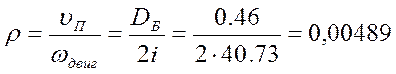           (м)

Приведенный момент инерции поступательно-движущегося груза:

          ;     ()

           (кг×м²)

Приведенный момент инерции пустого крюка:

                   ;     ()

           (кг×м²)

Зная радиус приведения, вычислим приведенное значение момента сопротивления:

           ;     ()

           (Н×м)

Момент потерь рассчитаем по формуле:

          ;     ()

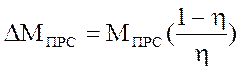при подъёме груза:

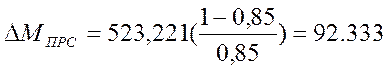           (Н×м)

Приведенная жёсткость каната между грузом и барабаном/5, с. 8/;

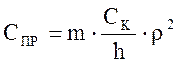;     (7.17)

здесь: m – кратность полиспаста; m=2;

          С_К- жесткость каната; С_К=2×10⁸ Н

           h – высота подъёма; h=15 м

           r - радиус приведения

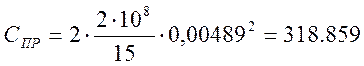           Н×м

Момент инерции двигателя и звеньев, жестко связанных с двигателем, вращающимися со скоркстями отличными или равными скорости двигателя:

          ;     ()

Момент инерции муфты типа МУВП 1-60:

           (кг×м²)

          (кг×м²)

Для исследования свойства этой системы как объекта управления примем возмущающее воздействие М_прс=0, D М_прс=0 и преобразуем структуру к следующему виду:

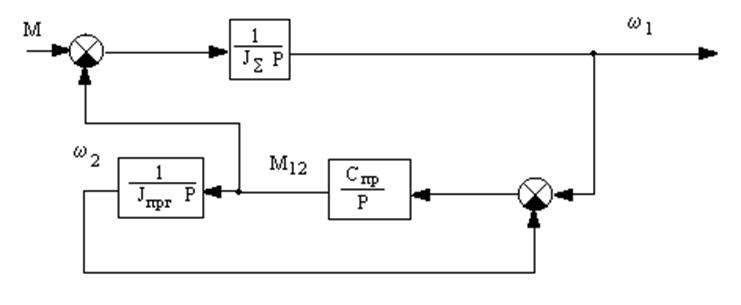
Рисунок 7 Преобразование структурной схемы механической части ЭП

Перенесем воздействие М₁₂ со входа звена с ПФ 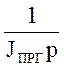 на его выход получим:

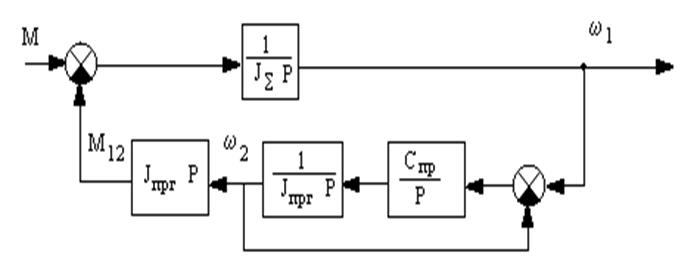
Рисунок 8. Продолжение структурных преобразований механической части              

                                                                    ЭП

Передаточная функция цепи ОС:

          ;     ()

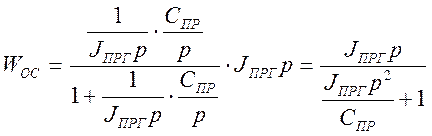Искомая придаточная функция:

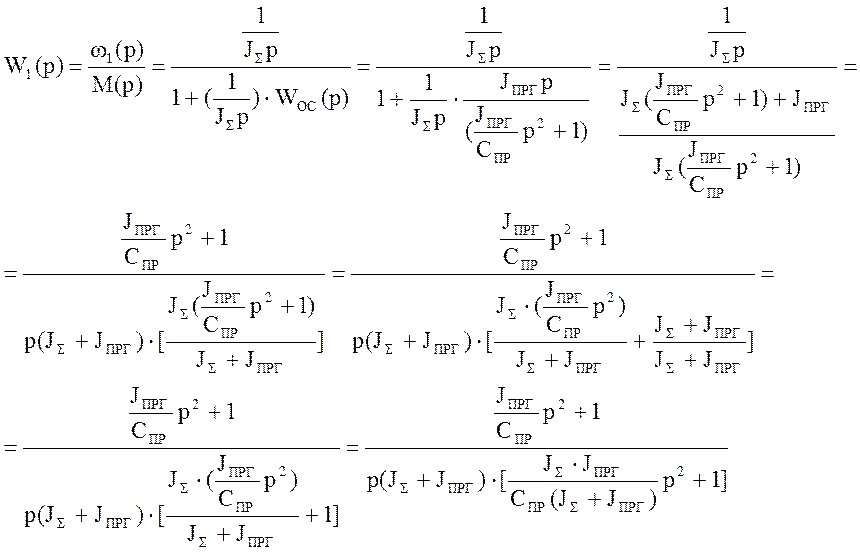
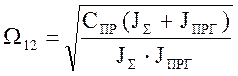 - резонансная частота схемы

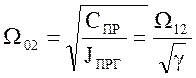           - резонансная частота массы при J_Σ à¥ 

Передаточная функция примет вид:

          ;     ()

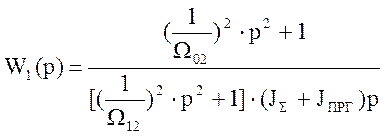Для анализа свойств системы воспользуемся её логарифмическими частотными характеристиками ЛАХ и ЛФХ. Частоты спряжения асимптоты ЛАХ равны:

;  

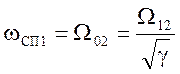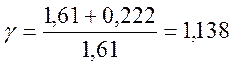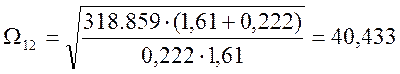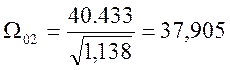          ;      (1/с)

           1\с

ω_сп1=37.905 с^-1_, ω_сп2=40.433 с^-1

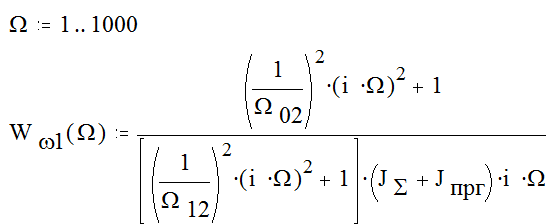
Для анализа свойств системы воспользуемся ее лагорифмическими частотными характеристиками ЛАХ и ЛФХ

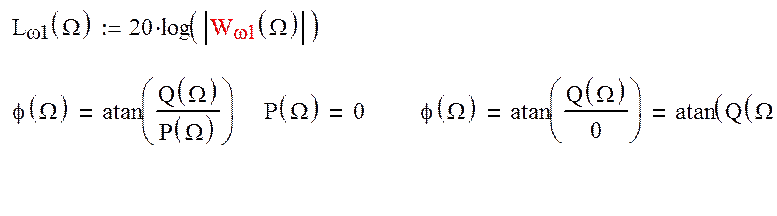
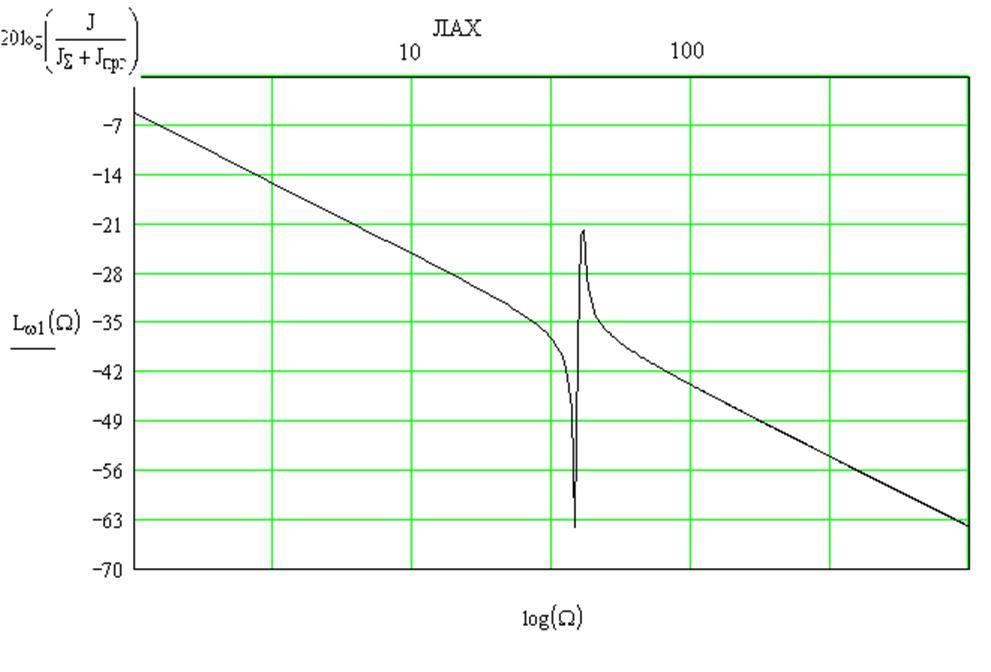
Рисунок 9.ЛАХ

В соответствии с передаточной функцией W₁(p) система может быть представлена последовательным соединением интегрирующего звена 2-го порядка с частотой сопряжения 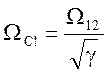 и консервативного звена с резонансной частотой . При  ЛАЧХ терпит разрыв, стремясь к - ¥; при амплитуда стремится к +¥, образуя второй разрыв.

          Низкочастотная амплитуда определяется интегрирующим звеном с коэффициентом обратно пропорциональным (J_прг+ J_S) и имеем наклон –20 об/дек.

          Высоко частотная асимптота () соответствует также интегрирующему звену, но при коэффициенте в g раз большем, чем в области низких частот. В этом можно убедиться при W ॠв формуле W_w1(p), при  p= g W.

          Так как частоты спряжения отличаются менее чем на 2 октавы, то значение частотных характеристик складываются алгебраически и влияние упругих связей на динамику электропривода можно пренебречь.

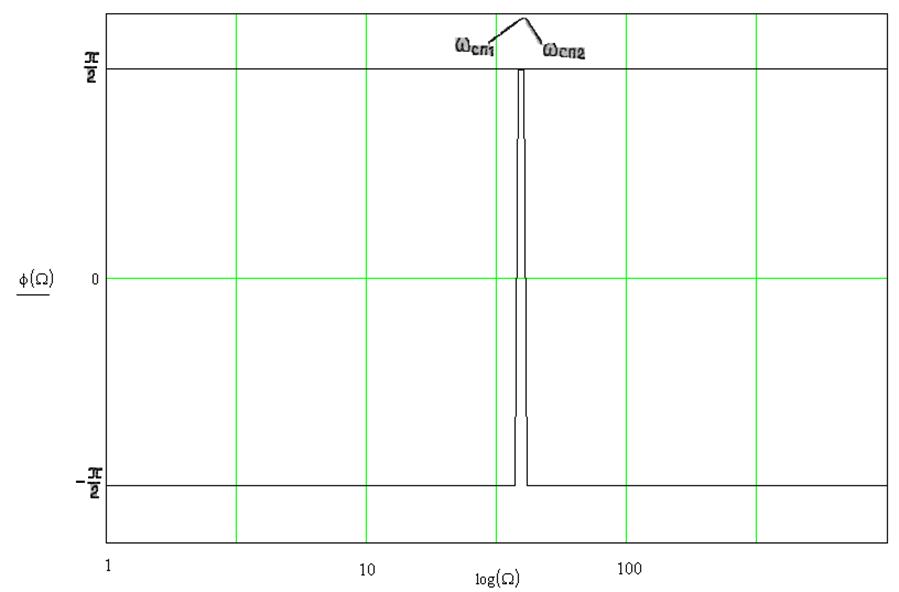
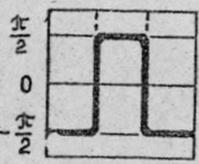
Рисунок 10.ЛФХ

Поскольку ,то движение приведенной массы близко к движению, определяемому интегрирующим звеном 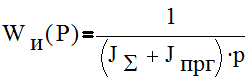 . Кроме того в рассматриваемом случае     , т.е. полюс передаточной функции  практически компенсируется ее нулем, следовательно, область частот, где имеет место фазовый сдвиг 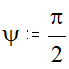 незначительна. Поэтому при отсутствии обратных связей по координатам второй маховой массы   для синтеза систем управления ЭП можно без заметной погрешности представить механическую часть привода жестким приведенным звеном.

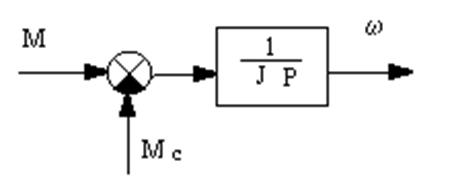
Рисунок 11. Структурная схема механической части электропривода с жёсткими связями

         

         8. Расчёт статических характеристик двигателя в требуемых режимах работы.

Построение естественной характеристики производится по формуле