ТЕПЛООБМЕН В ПОЛУРАДИАЦИОННЫХ И КОНВЕКТИВНЫХ ПОВЕРХНОСТЯХ НАГРЕВА
СИСТЕМА УРАВНЕНИЙ ЭНЕРГИИ ПО ГАЗАМ И РАБОЧЕМУ ТЕЛУ ПРИ ТЕПЛООБМЕНЕ
 Тепловой
расчет поверхностей нагрева парового котла производится на основе применения
аналитических методов и теории подобия к процессам теплообмена. При этом
учитываются все сложности процессов:
Тепловой
расчет поверхностей нагрева парового котла производится на основе применения
аналитических методов и теории подобия к процессам теплообмена. При этом
учитываются все сложности процессов:
сочетание радиационной и конвективной теплоотдачи от газового потока, присутствие твердых примесей в дымовых газах, сложный характер омывания поверхностей, наличие наружных и внутренних загрязнений, особенности формы поверхностей нагрева — ребристых, плавниковых труб, волнистых набивок РВП и т. д.
В расчете поверхностей нагрева, расположенных непосредственно за топочной камерой, например ширмовых, необходимо учитывать излучение, проникающее из топочной камеры. Такие поверхности называют полурадиационными. За ними по ходу газов располагают конвективные поверхности,
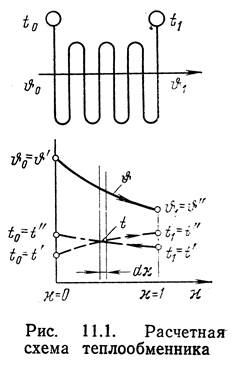
Для поверхности нагрева можно составить дифференциальные уравнения энергии по газам и рабочему телу. Изменение количества теплоты в элементе теплообменника длиной dx(рис. 11.1),
отданной газами и. воспринятой рабочим телом, равно количеству теплоты, переданной за счет теплопередачи. Без учета дополнительных источников теплоты за счет присосов и лучистой теплоотдачи из топки систему дифференциальных уравнений для газов и рабочего тела можно записать в виде
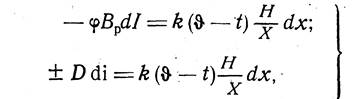
(11.1)
где Вр — расчетный расход топлива, кг/с; D — расход рабочего тела (пара, воды), кг/с; (φ—коэффициент сохранения теплоты; /—энтальпия газа, отнесенная к 1 кг топлива, кДж/кг; i—энтальпия рабочего тела, кДж/кг; k—текущее значение коэффициента теплопередачи, кВтм-2K-1; (θ-t)—текущее значение разности температур газа и рабочего тела (температурный напор). К; Н/Х—отношение поверхности к длине теплообменника, м2/м; х—текущее значение длины теплообменника по ходу газов, м.
В первом уравнении системы (11.1) знак минус показывает, что * энтальпия газов уменьшается по длине теплообменника. Во втором уравнении системы (11.1) знак плюс принимается для прямотока, знак минус—для противотока. Система (11.1) является нелинейной вследствие зависимости энтальпий и коэффициента теплопередачи от температуры.
Покажем, как может быть решена эта система, если в первом приближении пренебречь зависимостями теплоемкостей и коэффициента теплопередачи от температуры. Дифференциалы энтальпий можно представить как
![]() (11.2)
(11.2)
![]() , (11.3)
, (11.3)
где Vг—объем газов, отнесенный к 1 кг топлива, м3/ кг; Сг—теплоемкость газов, (кДж/м3 К); с—теплоемкость рабочего тела, кДж/(кгК). Систему (11.1) удобно записать в виде
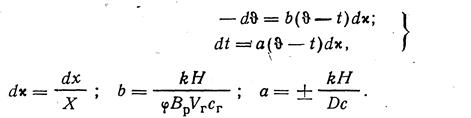
Способ решения системы (11.4), принятый в нормативном методе теплового расчета котельных агрегатов, заключается в приведении двух дифференциальных уравнений для температур к одному уравнению для температурных 'напоров. Вычитая почленно уравнения системы (11.4), можно получить
![]() (11.5)
(11.5)
ИЛИ
![]() (11.6)
(11.6)
Обозначим температуры при χ=0 буквами 0'о и /о и при »χ=1 буквами θ1 и t1. Проинтегрируем уравнение (11.5), считая а и b постоянными:
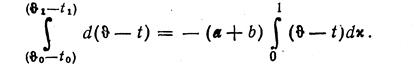 (11.7)
(11.7)
Интеграл в правой части обозначим как среднеинтегральный температурный
напор Δt
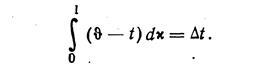 (11.8)
(11.8)
Тогда уравнение (11.7) после интегрирования левой» части запишется в виде
![]() (11.9) Запишем интеграл
уравнения (11.6)
(11.9) Запишем интеграл
уравнения (11.6)
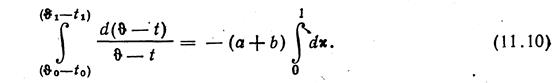
В результате интегрирования получим
![]()
Из выражений ^11.9) и (11.11) исключим —(а-}-Ь). Тогда
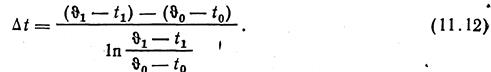
Полученное выражение в теории теплопередачи получило название
среднелогарифмического
температурного напора. В выражении (11.9) значение ![]() подставляется
из формулы (11.12), а величина k в выражениях а и b обычно
вычисляется по среднеарифметическим значениям температур газа и рабочего тела.
Такой способ решения дифференциальных уравнений энергии для теплообменников
удобен для ручного расчета. Для поверочных расчетов паровых котлов на ЭВМ
применяются другие методы решений уравнений энергии (см. гл.
16), . Интегралы уравнений системы (11.4) можно
представить в виде
подставляется
из формулы (11.12), а величина k в выражениях а и b обычно
вычисляется по среднеарифметическим значениям температур газа и рабочего тела.
Такой способ решения дифференциальных уравнений энергии для теплообменников
удобен для ручного расчета. Для поверочных расчетов паровых котлов на ЭВМ
применяются другие методы решений уравнений энергии (см. гл.
16), . Интегралы уравнений системы (11.4) можно
представить в виде

Обозначив ![]() и,
кроме того,
и,
кроме того, ![]() для прямотока, а
для прямотока, а ![]() для
противотока (рис. 11.1) и раскрыв значения а и Ь, получим:.
для
противотока (рис. 11.1) и раскрыв значения а и Ь, получим:.![]()
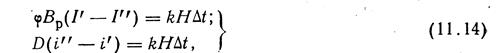
где левые части уравнений выражают соответственно, количество теплоты, переданной газами и воспринятой рабочим телом по балансу, а правые -количество теплоты, переданной за счет теплопередачи. Эти количества теплоты обычно относят к единице расхода топлива. Тогда баланс теплоты по газам, рабочему телу и теплопередаче выразится как
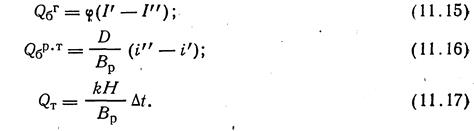
При необходимости в формулах (11.15), (11.16) следует учесть, дополнительные источники теплоты—присосы и излучение из топки:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.