Расчет паровой турбины К-600-6,3 для одноконтурной АЭС, страница 8

8)       Определим окружную скорость для последней ступени в группе:

 ,м/с

u=3,142·1,65·50=259,2м/с;                                                                                                           

9)       Теплоперепад последней ступени в группе:

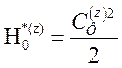 ,кДж/кг, где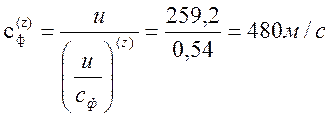

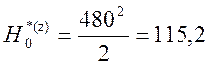 кДж/кг.

10)     Определение среднего теплоперепада от параметров торможения в группе:

Средний теплоперепад найдём по теореме о среднем:

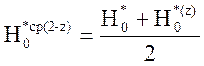,  кД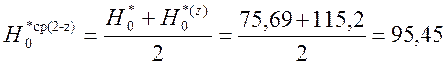ж/кг.                                                                           

 Дж/кг

11)            Определение числа ступеней в группе:

Расчет числа ступеней ЧНД

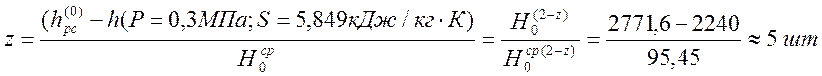
Задаемся начальными параметрами, которые берем из прототипа:

ρ = 0,3; d^(z) = 2350 мм; l^(z) = 0,852 м; [10]

Геометрически по чертежу прототипа находим :

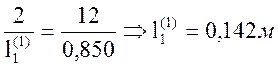
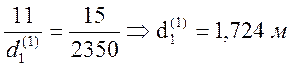
Расчет первой ступени в группе:

ρ = 0,3;  d⁽¹⁾ = 1,724 м; l⁽¹⁾ = 0,140 м;

1. 

Рассчитаем отношение :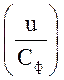

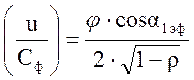
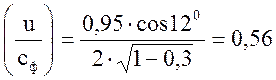
2. Определим окружную скорость:

 ,м/с.                                                                                    

м/с

3. Теплоперепад последней ступени в группе:

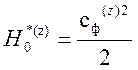,кДж/кг,        где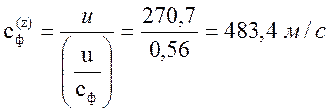; 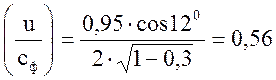м/с

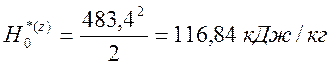
4.

0, 748 м³/кг

·К

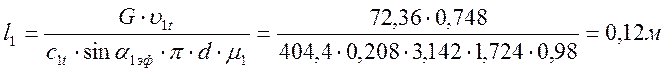
5.            Определение корневого диаметра:

,м            

  

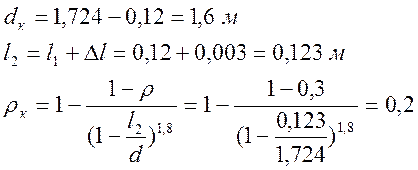
l₂ - длина рабочей лопатки первой ступени группы:

6.  d^(z) = 2350 мм; l^(z) = 0,852 м;

d_к= 1600 мм

Определим окружную скорость для последней ступени в группе:

 ,м/с.

Тепловой расчет последней ступени турбины

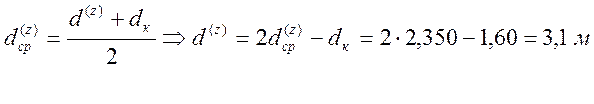
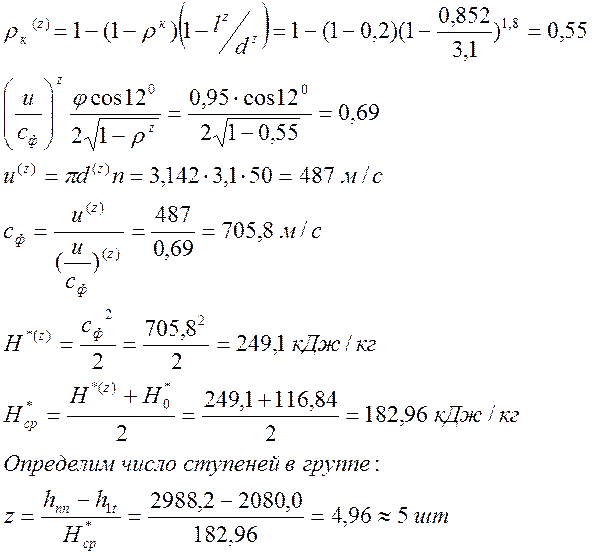
1.  Параметры пара перед сопловой решеткой:

h₀=2575,0 кДж/кг;

По энтальпии на выходе и давлению из рабочей решетки находим энтропию

s=7,68 кДж/(кг×К)

По полученной энтропии и энтальпии  находим давление на входе

P₀=0,0275 МПа; ρ = 0,501; G = 72,36 кг/с; α₁ = 12⁰

2.  Определение окружной скорости и располагаемого теплоперепада от параметров торможения:

Диаметр d = 3,1 м – взят из расчёта числа ступеней ЧНД.

Окружная скорость: , м/с.                                                            

          где  - число оборотов турбины.

          u =3,142·3,1·50=486,7 м/с.

3.  Принимаем степень реактивности r = 0,501, коэффициент скорости j = 0,95 и угол направления a₁ =  12⁰ [10]

4. Отношение 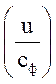 =  0,657;

     Тогда фиктивная скорость 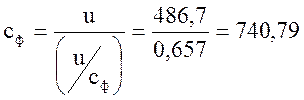 м/с.                    

Теплоперепад 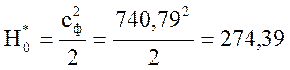  кДж/кг.                                                       

5.  Определим параметры:

Теплоперепад, срабатываемый на сопловой решетке:

Н*_ос = (1-r)× Н*₀ ,  кДж/кг.                                                                      

Н*_ос= (1-0,501)×274,7 = 137,1 кДж/кг.

Теплоперепад, срабатываемый на рабочей решетке:

Н*_ор = r× Н*₀ ,кДж/кг.                                                                                        

Н*_ор= 0,501×274,7 = 137,6 кДж/кг.

Найдем теплофизические параметры пара:

Теоретическая энтальпия на выходе из сопловой решетки:

h_1t = h*₀ - Н*_oc ,кДж/кг.                                                                                      

h_1t =2575 – 137,1 = 2437,9 кДж/кг.

Давление на выходе из сопловой решетки:

 P₁(h_1t=2438 кДж/кг; S₀ = 7,68 кДж/кг ⁰C) = 0,011 МПа

Теоретическая энтальпия на выходе из рабочей решетки:

h_2t’ = h*₀ - Н*₀  кДж/кг.                                                                                      

h_2t’=2575 – 274,39 = 2300,6 кДж/кг.

Давление на выходе из рабочей решетки:

P₂(h_2t’=2300,6 кДж/кг; S₀ = 7,68 кДж/кг ⁰C) = 0,004 МПа

Удельный объем  на выходе из сопловой решетки:

u_1t(h_1t=2438 кДж/кг; S₀ = 7,68 кДж/кг ⁰C) = 13,67 м³/кг.

Удельный объем  на выходе из рабочей решетки:

u_2t’(h_2t’=2300,6 кДж/кг; S₀ = 7,68 кДж/кг ⁰C) = 31,17 м³/кг.

Температура на выходе из сопловой решетки:

t_1t(h_1t=2438 кДж/кг; S₀ = 7,68 кДж/кг ⁰C) = 45,81  ⁰C.

Температура на выходе из рабочей решетки:

t_2t’(h_2t’=2300,6 кДж/кг; S₀ = 7,68 кДж/кг ⁰C) = 28,96  ⁰C.

6.  Определение площади выхода сопловой решетки:

Отношение давлений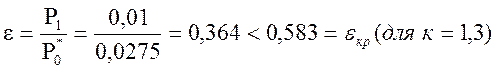                                                  

Решетка сопловая сверхзвуковая.

Принимаем в первом приближении коэффициент расхода          [10]

Расход пара: G = 72,36 кг/с.                                                  (10)