Исходные данные:
Тип турбогенератора: ТВВ-200-2
Pном = 200МВт cosφ=0.85 x”d=0,19 x2=0,23 r =0,002 ое Uном=15,75кВ
Pо/Pном=1
Принимаем xd=1,88
1. Расчет нормального режима ТГ, построение векторной диаграммы и угловой характеристики при Pг=0,2 Р’ген
 Весь расчет будем вести в относительных
единицах, но в случае необходимости будем прибегать к именованным. В качестве
базисных величин принимаем номинальную мощность генератора и напряжение
системы.
Весь расчет будем вести в относительных
единицах, но в случае необходимости будем прибегать к именованным. В качестве
базисных величин принимаем номинальную мощность генератора и напряжение
системы.
Рисунок 1- Схема замещения
Sном=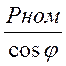 Sном=
Sном=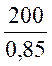 =235,3МВт
=235,3МВт
Xвн=(0,3…0,5) xd = (0,3…0,5) 1,88 =0,564…0,94
Принимаем Xвн=0,7
Uг=1,04 Sбаз= Sном Uс=1
Р’ген=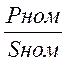 =
=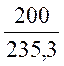 =0,85
=0,85
1.1. Определение реактивной мощности генератора
Pг=0,2![]() Р’ген=0,2
Р’ген=0,2![]() 0,85= 0,17
0,85= 0,17
Uс=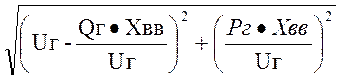
1=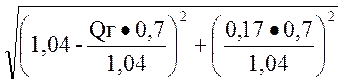
0,45![]() Qг2 - 1,4
Qг2 - 1,4![]() Qг + 0,09 = 0
Qг + 0,09 = 0
a = 0,45 b = -1,4 c = 0,09
D = b2 – 4 a c = 1,798
Q1
= 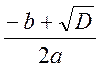 =
=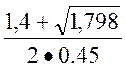 =3,045439
=3,045439
Q2
= 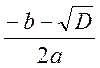 =
=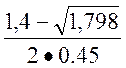 = 0,065672
= 0,065672
т.к. реактивная мощность не может превышать активную, то в качестве реактивной мощности принимаем:
Qг = Q2 = 0,065672
1.2. Полная мощность синхронного генератора
Sг=![]() =
= ![]() =0,182244
=0,182244
1.3. Определение тока статора генератора
Iг=![]() =
=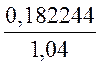 = 0,17523
= 0,17523
1.4. Внутренний угол генератора
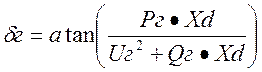 =
=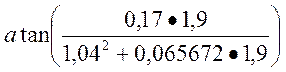 =14,989, град
=14,989, град
1.5. Определение cosφ генератора
φг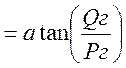 =
=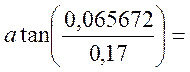 21,1218, град
21,1218, град
1.6.
Угол между Еq и Iг - ![]()
![]() =
= ![]() + φг = 14,989 + 21,1218 =
36,1109, град
+ φг = 14,989 + 21,1218 =
36,1109, град
1.7. Составляющие Iг и Uг в осях d и q
Uгd = Uг![]() sin(
sin(![]() ) = 1,04
) = 1,04![]() sin(14,989) = 0,26898
sin(14,989) = 0,26898
Uгq = Uг![]() cos(
cos(![]() ) = 1,04
) = 1,04![]() cos(14,989) = 1,00461
cos(14,989) = 1,00461
Iгd = Iг![]() sin(φг) = 0,17523
sin(φг) = 0,17523![]() sin(21,1218)
= 0,10327
sin(21,1218)
= 0,10327
Iгq = Iг![]() cos(φг) = 0,17523
cos(φг) = 0,17523![]() cos(21,1218)
= 0,14157
cos(21,1218)
= 0,14157
Проверка:
Xq = Xd
Uгd = Iгd![]() Xq
= 0,10327
Xq
= 0,10327 ![]() 1,9 = 0,26898
1,9 = 0,26898
Pг = Uгd![]() Iгd +
Uгq
Iгd +
Uгq ![]() Iгq = 0,26898
Iгq = 0,26898![]() 0,10327
+ 1,00461
0,10327
+ 1,00461![]() 0,14157 = 0,17
0,14157 = 0,17
1.8. Расчет Eq
Eq =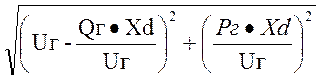 =
=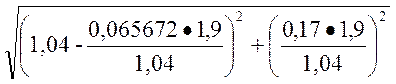 = 0,97103
= 0,97103
1.9. Определение угла δΣ между Eq и Uс
ΔQ = Iг![]() Xвн
= 0,17523
Xвн
= 0,17523 ![]() 0,7 = 0,02149
0,7 = 0,02149
Qc=Qг – ΔQ = 0,0656720 – 0,02149 = 04418
Pc = Pг
δвн = atan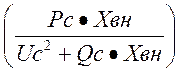 = atan
= atan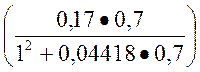 = 6,58454, град
= 6,58454, град
δΣ =δг + δвн = 14,989 + 6,58454 = 21,5736 град
1.10. Угловая характеристика
 Pг0.2(δ)
=
Pг0.2(δ)
= 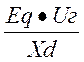 sin (δ) =
sin (δ) = 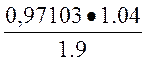 sin (δ) = 0,53151 sin (δ)
sin (δ) = 0,53151 sin (δ)
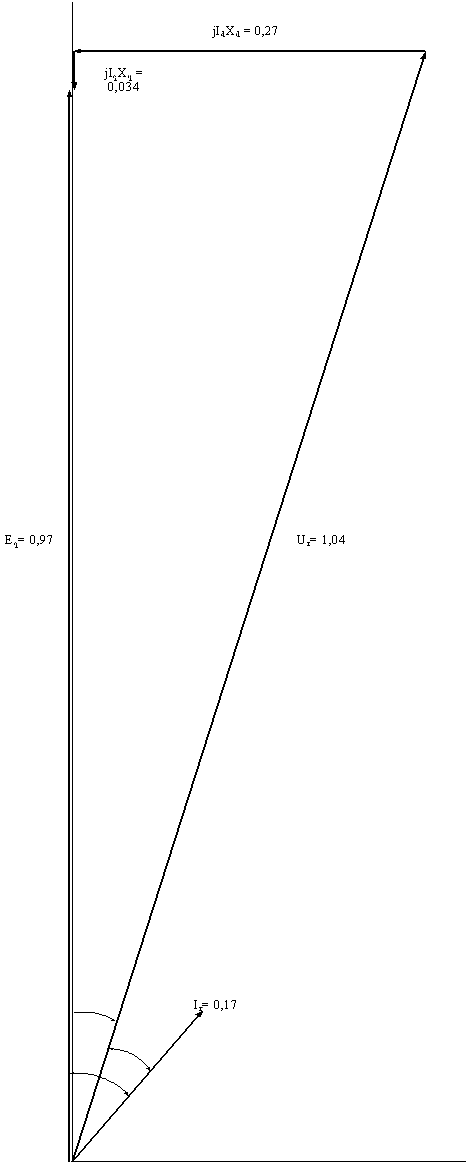
Рисунок 2- Векторная диаграмма при Pг=0,2 Р’ген
2. Расчет нормального режима ТГ, построение векторной диаграммы и угловой характеристики при Pг=0,4 Р’ген
2.1. Определение реактивной мощности генератора
Pг=0,4![]() Р’ген=0,4
Р’ген=0,4![]() 0,85= 0,34
0,85= 0,34
Uс=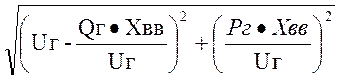
1=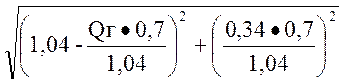
0,45![]() Qг2 - 1,4
Qг2 - 1,4![]() Qг + 0,13 = 0
Qг + 0,13 = 0
a = 0,45 b = -1,4 c = 0,13
D = b2 – 4 a c = 1,719
Q1
= 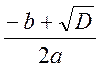 =
=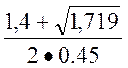 =3,01228
=3,01228
Q2
= 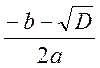 =
=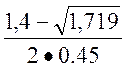 = 0,09883
= 0,09883
т.к. реактивная мощность не может превышать активную, то в качестве реактивной мощности принимаем:
Qг = Q2 = 0,09883
2.2. Полная мощность синхронного генератора
Sг=![]() =
= ![]() =0,35407
=0,35407
2.3. Определение тока статора генератора
Iг=![]() =
=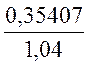 = 0,34046
= 0,34046
2.4. Внутренний угол генератора
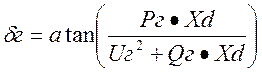 =
=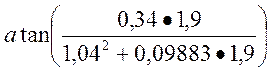 =26,97, град
=26,97, град
2.5. Определение cosφ генератора
φг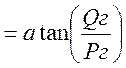 =
=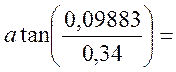 16,2084, град
16,2084, град
2.6.
Угол между Еq и Iг - ![]()
![]() =
= ![]() + φг = 26,97 + 16,2084 = 43,18,
град
+ φг = 26,97 + 16,2084 = 43,18,
град
2.7. Составляющие Iг и Uг в осях d и q
Uгd = Uг![]() sin(
sin(![]() ) = 1,04
) = 1,04![]() sin(26,97) = 0,4717
sin(26,97) = 0,4717
Uгq = Uг![]() cos(
cos(![]() ) = 1,04
) = 1,04![]() cos(26,97) = 0,92688
cos(26,97) = 0,92688
Iгd = Iг![]() sin(φг) = 0,17523
sin(φг) = 0,17523![]() sin(16,2084)
= 0,23297
sin(16,2084)
= 0,23297
Iгq = Iг![]() cos(φг) = 0,17523
cos(φг) = 0,17523![]() cos(16,2084)
= 0,24826
cos(16,2084)
= 0,24826
Проверка:
Xq = Xd
Uгd = Iгd![]() Xq
= 0,23297
Xq
= 0,23297 ![]() 1,9 = 0,4717
1,9 = 0,4717
Pг = Uгd![]() Iгd +
Uгq
Iгd +
Uгq ![]() Iгq = 0,4717
Iгq = 0,4717![]() 0,23297
+ 0,92688
0,23297
+ 0,92688![]() 0,24826 = 0,34
0,24826 = 0,34
2.8. Расчет Eq
Eq =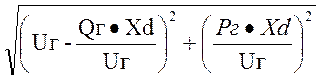 =
=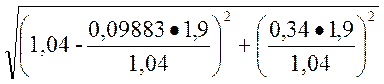 = 1,06
= 1,06
2.9. Определение угла δΣ между Eq и Uс
ΔQ = Iг![]() Xвн
= 0,34046
Xвн
= 0,34046 ![]() 0,7 = 0,08114
0,7 = 0,08114
Qc=Qг – ΔQ = 0,09883 – 0,08114 = 0,0177
Pc = Pг
δвн = atan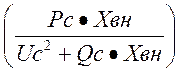 = atan
= atan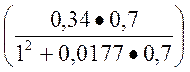 = 13,22, град
= 13,22, град
δΣ =δг + δвн = 26,97 + 13,22 = 40,2013 град
2.10. Угловая характеристика
 Pг0.4(δ)
=
Pг0.4(δ)
= 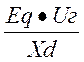 sin (δ) =
sin (δ) = 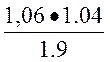 sin (δ) = 0,58 sin (δ)
sin (δ) = 0,58 sin (δ)
Рисунок 3- Векторная диаграмма при Pг=0,4 Р’ген
3. Расчет нормального режима ТГ, построение векторной диаграммы и угловой характеристики при Pг=0,6 Р’ген
3.1. Определение реактивной мощности генератора
Pг=0,6![]() Р’ген=0,6
Р’ген=0,6![]() 0,85= 0,51
0,85= 0,51
Uс=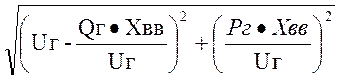
1=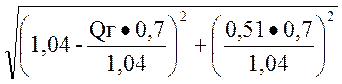
0,45![]() Qг2 - 1,4
Qг2 - 1,4![]() Qг + 0,199 = 0
Qг + 0,199 = 0
a = 0,45 b = -1,4 c = 0,199
D = b2 – 4 a c = 1,6
Q1 = 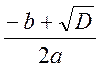 =
=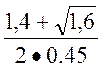 =2,98
=2,98
Q2 = 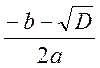 =
=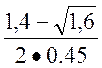 = 0,15
= 0,15
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.