






Введение
Дифференциальные уравнения, описывающие процесс теплообмена в элементе Филда нелинейные, в связи с этим необходимо вычислить поверхность рекуператора методом сеток.
Рассматриваемый
элемент делится на участки длиной ![]() (чем выше требуемая
точность вычислений, тем меньше
(чем выше требуемая
точность вычислений, тем меньше ![]() ).
).
Средние
температуры стенок рассматриваемого участка ![]() ,
получают из балансов тепловых потоков. После вычислений этих температур, можно
определить прирост температур теплоносителя во внутренней трубе и в кольцевом
пространстве, а затем приступают с вычислению температур на следующем
,
получают из балансов тепловых потоков. После вычислений этих температур, можно
определить прирост температур теплоносителя во внутренней трубе и в кольцевом
пространстве, а затем приступают с вычислению температур на следующем ![]() участке.
участке.
Распределение температур в элементе Филда.
Рис.1
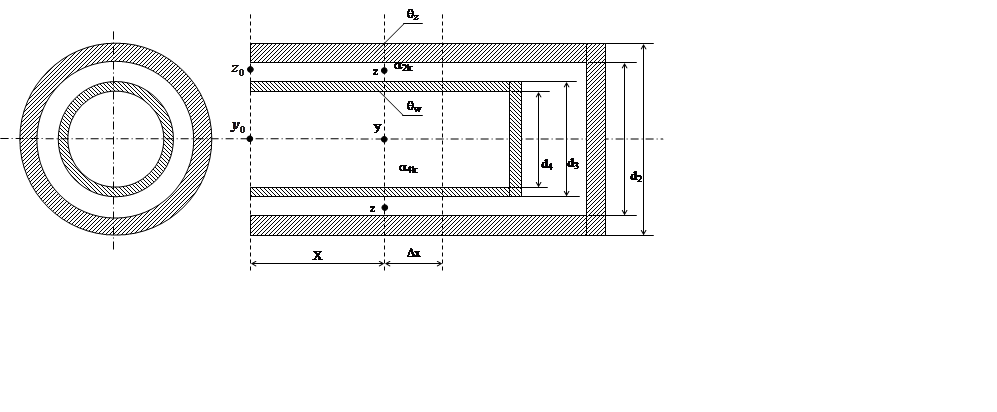
Исходные данные:
1.
Скорость воздуха: ![]() м/с.
м/с.
2.
Температура продуктов сгорания:![]() =1210 °С.
=1210 °С.
3.
Температуры воздуха: ![]() °С
°С
![]() °С
°С
4.
Длина участка: ![]() мм =0,05м.
мм =0,05м.
5. Геометрические размеры:
![]() мм =0,072м.
мм =0,072м.
![]() мм =0,067 м.
мм =0,067 м.
![]() мм =0,44м.
мм =0,44м.
![]() мм =0,042 м.
мм =0,042 м.
1.1. Определение коэффициента теплоотдачи сложного теплообмена со стороны потока газов:
![]() ,
, ![]() .
.
где
![]() - радиационный коэффициент теплоотдачи,
- радиационный коэффициент теплоотдачи, ![]() ;
;
![]() - конвективный коэффициент теплоотдачи,
- конвективный коэффициент теплоотдачи, ![]() ;
;
1.1.1. Вычисление радиационного коэффициента теплоотдачи:
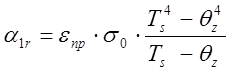
где
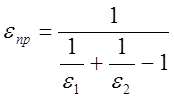 - приведенная степень черноты:
- приведенная степень черноты:
![]() - степень черноты продуктов сгорания;
- степень черноты продуктов сгорания;
![]() - степень черноты металла;
- степень черноты металла;
Отсюда
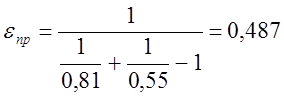
![]() - постоянная Стефана – Больцмана,
- постоянная Стефана – Больцмана, ![]() ;
;
![]() К – средняя температура продуктов сгорания;
К – средняя температура продуктов сгорания;
![]() - средняя температура внешней стенки
металла, К;
- средняя температура внешней стенки
металла, К;
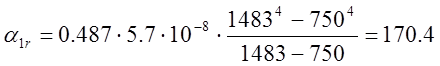
![]() .
.
1.1.2. Определение чисел Рейнольдса и Нуссельта:
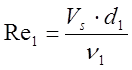
где
![]() м2/с – кинематическая вязкость
дымовых газов.
м2/с – кинематическая вязкость
дымовых газов.
Здесь и в дальнейшем теплофизические свойства воздуха и дымовых газов взяты из [1].
![]() - скорость газов, м/с.
- скорость газов, м/с.
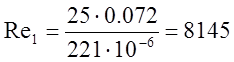 > Reкр=1000 Следовательно течение турбулентно.
> Reкр=1000 Следовательно течение турбулентно.
![]()
![]() - число Прандтля для дымовых газов.
- число Прандтля для дымовых газов.
![]()
Коэффициент
теплоотдачи: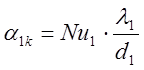 ,
, ![]()
где
![]() коэффициент теплопроводности,
коэффициент теплопроводности, ![]() ;
;
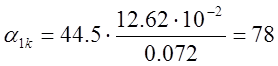
![]()
Отсюда
по пункту 1.1.: ![]() ,
, ![]() .
.
1.2. Определение конвективного коэффициента теплоотдачи на
поверхности 2 -![]() ,
, ![]() .
.
1.2.1. Определение расхода воздуха:
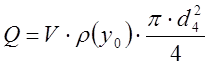
где
![]() =
=![]() кг/м3 –
плотность воздуха.
кг/м3 –
плотность воздуха.
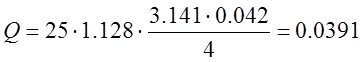 кг/с.
кг/с.
1.2.2. Скорость в кольце:
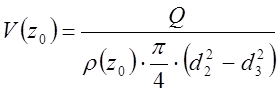 , м/с.
, м/с.
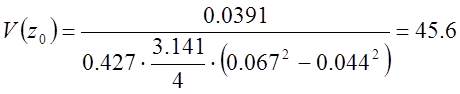 м/с.
м/с.
Число
Рейнольдса: 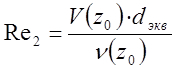
где
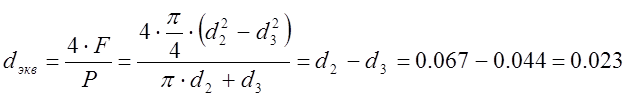 м.
м.
Отсюда
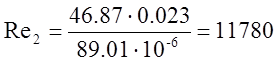 - течение турбулентное.
- течение турбулентное.
Число
Нуссельта: ![]()
где
![]() - поправка на начальный участок.
- поправка на начальный участок.
Pr2 =0,694 – число Прандтля для воздуха.
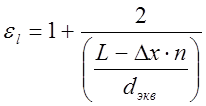
где L=1,0 м – длина элемента Филда (принимаем в первом приближении)
n - номер рассматриваемого участка.
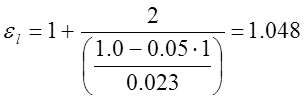
Отсюда ![]()
Тогда 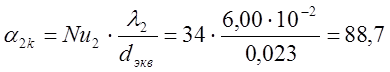
![]() .
.
Параметры
![]() ,
, ![]() ,
, ![]() ,
, ![]() -
определяем по таблицам, приведенным в [1], для каждого участка z =555°C.
-
определяем по таблицам, приведенным в [1], для каждого участка z =555°C.
1.3. Определение конвективного коэффициента теплоотдачи на
поверхности 3 -![]() ,
, ![]() .
.
Число Нуссельта: 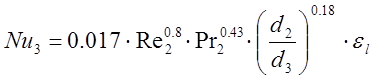
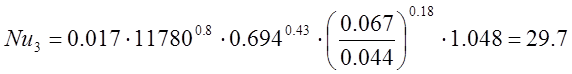
Тогда 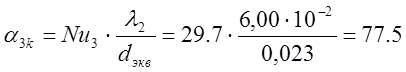
![]() .
.
1.4. Определение конвективного коэффициента теплоотдачи на
поверхности 4 -![]() ,
, ![]() .
.
Скорость воздуха в трубе:
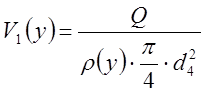 , м/с.
, м/с.
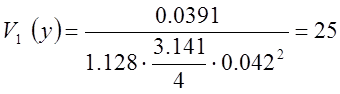 м/с.
м/с.
где
![]() – средняя температура во внутренней трубе, °С.
– средняя температура во внутренней трубе, °С.
Параметры
![]() ,
, ![]() ,
, ![]() ,
, ![]() -
определяем по таблицам, приведенным в [1].
-
определяем по таблицам, приведенным в [1].
Число
Рейнольдса: 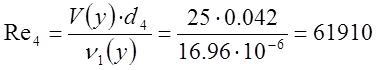
Число
Нуссельта: ![]()
Отсюда
![]()
Тогда
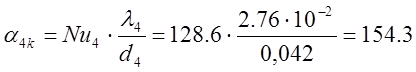
![]() .
.
1.5. Определение потока тепла, отнесенного к единице трубы от потока продуктов сгорания к поверхность внутренней трубы:
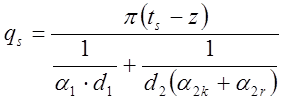 , Вт/м.
, Вт/м.
где
![]() - эквивалентный радиационный коэффициент
теплоотдачи, при первой итерации принимаем
- эквивалентный радиационный коэффициент
теплоотдачи, при первой итерации принимаем ![]() ;
;
![]() - средняя температура в кольцевом
пространстве нагреваемого теплоносителя, °С.
- средняя температура в кольцевом
пространстве нагреваемого теплоносителя, °С.
Проводя расчет методом последовательных
приближений, для последней итерации принимаем ![]()
![]() .
.
Тогда 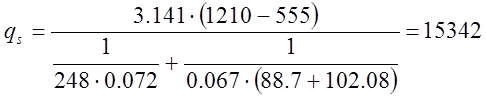 Вт/м.
Вт/м.
1.6. Первое приближение значения температуры внешней стенки составит:
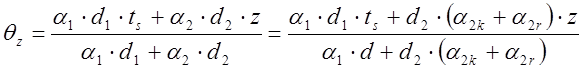
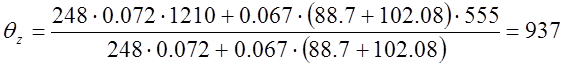 °С.
°С.
1.7. Конвективный поток тепла от наружной трубы:
![]() , Вт/м.
, Вт/м.
![]() , Вт/м.
, Вт/м.
1.8. Остаток тепла, передаваемый от наружной трубы к внутренней радиацией составляет:
![]() , Вт/м.
, Вт/м.
1.9. Из баланса потока тепла находим первое приближение температуры стенки внутреннего цилиндра:
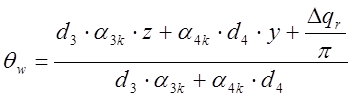 , °С.
, °С.
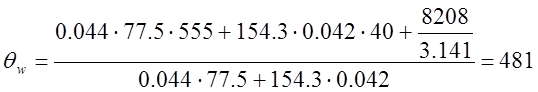 °С.
°С.
1.10. Уточним значение радиационного потока между трубами:
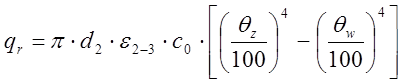 ,
Вт/м.
,
Вт/м.
где с0 =5,67.
![]() -
приведенная степень черноты;
-
приведенная степень черноты;
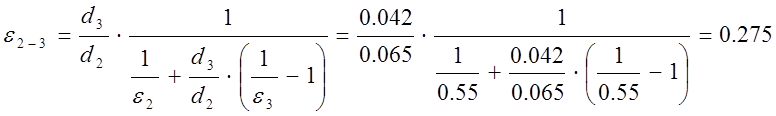
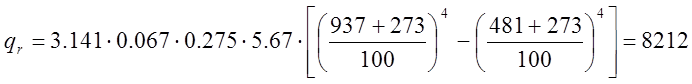 Вт/м.
Вт/м.
1.11. Сравнение
![]() и
и ![]() :
:
Если 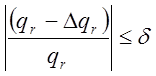 ,
,
где ![]() -
принятая точность вычислений, то вычисляем исправленное значение
-
принятая точность вычислений, то вычисляем исправленное значение 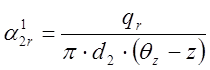 и возвращаемся к пункту 1.5.
и возвращаемся к пункту 1.5.
 и
последующих итераций не требуется.
и
последующих итераций не требуется.
1.12.
Теплоемкость потока, нагреваемого теплоносителем, определяется
через ![]() и
и ![]() :
:
![]() ;
; ![]()
где
![]() и
и ![]() -
соответственно теплоемкости воздуха при температурах
-
соответственно теплоемкости воздуха при температурах ![]() и
и
![]() .
.
![]()
![]()
1.13. После
вычисления температур ![]() и
и ![]() для отрезка
для отрезка ![]() , определяем приросты температур
, определяем приросты температур ![]() и
и ![]() на этом участке.
на этом участке.
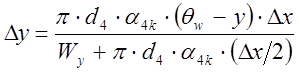 , °С
, °С
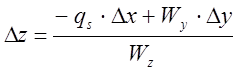 , °С.
, °С.
Отсюда 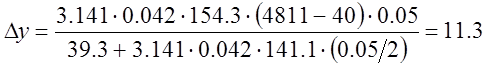 °С
°С
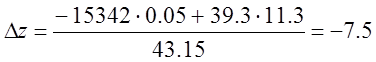 °C.
°C.
1.14. После
вычисления ![]() и
и ![]() получим начальные величины
получим начальные величины ![]() и
и ![]() для очередного участка
для очередного участка ![]() и проводим подобный расчет.
и проводим подобный расчет.
![]() °С.
°С.
![]() °С.
°С.
Когда ![]() расчет считается законченным.
расчет считается законченным.
Сведем рассчитанные участки в таблицу:
|
L, м |
qs , Вт/м |
|
|
y |
z |
|
0.05 |
15341 |
937 |
481 |
51 |
547 |
|
0.1 |
15367 |
936 |
494 |
63 |
539 |
|
0.15 |
15386 |
936 |
508 |
75 |
530 |
|
0.20 |
15420 |
935 |
521 |
87 |
520 |
|
0.25 |
15459 |
935 |
531 |
99 |
510 |
|
0.30 |
15502 |
934 |
541 |
111 |
499 |
|
0.35 |
15572 |
932 |
553 |
123 |
488 |
|
0.40 |
15602 |
932 |
564 |
136 |
476 |
|
0.45 |
15686 |
931 |
576 |
149 |
463 |
|
0.50 |
15767 |
929 |
586 |
162 |
450 |
|
0.55 |
15838 |
928 |
595 |
175 |
436 |
|
0.60 |
15924 |
926 |
608 |
188 |
421 |
|
0.65 |
16019 |
924 |
622 |
201 |
405 |
|
0.70 |
16142 |
922 |
627 |
215 |
388 |
|
0.75 |
16259 |
920 |
633 |
229 |
370 |
|
0.80 |
16350 |
919 |
646 |
243 |
351 |
|
0.85 |
16487 |
916 |
648 |
257 |
331 |
|
0.90 |
16539 |
913 |
651 |
269 |
307 |
|
0.95 |
16654 |
910 |
654 |
279 |
278 |
1. Исаченко В.П. , Осипова В.А. , Сукомел А.С. Теплопередача. –М. : Энергия, 1975. – 488 с.
Министерство общего и профессионального образования Российской Федерации
Новосибирский Государственный Технический Университет
Кафедра тепловых электрических станций
Расчетно – графическая работа
“Элемент Филда ”
Факультет: ФЭН
Группа: ТЭ-71
Студент: Чернышев А.
Преподаватель: Овчинников Ю.В.
Дата сдачи: 27.05.2001
Отметка о защите:
НОВОСИБИРСК 2001
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.