Фазовые переходы. Фазовое равновесие в двухфазной системе

9. Фазовые переходы

Фазовое равновесие в двухфазной системе. Фазой называется гомогенная (однородная) часть вещества, отделенная от другой границей раздела. Рассмотрим двухфазную систему, состоящую из жидкости и её пара, помещенную в замкнутый объем V при температуре T. Свободная энергия такой системы зависит от распределения вещества между фазами и положения границы раздела: . Здесь  и  – объёмы занятые жидкостью и паром соответственно, а  и  –  содержащиеся в них количество молей (частиц), причем

                          (256)

В этих условиях в термостатированной (T= const) системе реально изменяемыми являются две переменные, например,  и . Именно от них зависит распределение вещества между объемами, занятыми жидкой фазой и паром соответственно, при постоянных значениях величин , V и T.

Действительно, свободная энергия двухфазной системы при наличии идеальной границы есть

                                                      (257)

причем

                    (258)

так что с учетом законов сохранения (256) и того, что получим

  259)

Если система замкнута и термостатирована, то согласно неравенству (143) имеем

                                  (260)

и при приходе к равновесию, когда  , имеем

                                  (261)

          Первое из равенств (261) является условием гидростатического равновесия: давление на поверхность жидкости с обеих сторон должно быть одинаковым, чтобы она не пришла в движение. Если же поверхность смещена в ту или иную сторону относительно равновесного положения, то одна из фаз сжата, а другая – расширена. Возникающая разность давлений стремиться вернуть границу в прежнее положение. Возникает смещение  того же знака что и направляющее усилие, равное , и тогда , т. е. свободная  энергия  убывает до тех пор, пока величина  не станет равной нулю.

          Чтобы понять условие химического равновесия в равенствах (261), надо оставить границу раздела в покое, но учесть, что она прозрачна для молекул, переходящих из фазы в фазу. Если химический потенциал в одной фазе больше, чем в другой, то число частиц в ней начнет убывать, а в другой фазе – возрастать. Свободная энергия будет падать пока вещество не распределится между фазами таким образом, чтобы средние энергии на одну частицу (на один моль) сравнялись, как того требует  второе из равенств (261).

          Сформулировать условия равновесия можно и в том случае, если фиксированы не величины T  и V, а величины Tи p. Однако минимизируется в этом случае не свободная энергия, а термодинамический потенциал

                   (262)

Учитывая, что

                                    (263)

и  из уравнения (259) при    получим

        (264)

В результате воспроизводятся прежние условия (261):

                         (265)

с тем лишь уточнением, что не только давления жидкости и пара равны друг другу, но и точно таким же должно быть и внешнее давление p на систему, если мы хотим поддерживать ее в состоянии равновесия. Это давление есть давление насыщенного пара .

          Представляет интерес, каким образом удовлетворяются оба условия (265). Учтем, что согласно соотношениям (250) и (140)

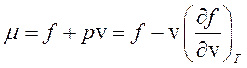,                                  (266)

причем это соотношение имеет место в какой угодно точке на изотерме. Но газ не переходит непрерывно в жидкость, а сосуществует с ней на одной изотерме, причем положение обеих точек выбирается так, чтобы одновременно выравнивались и химические потенциалы, и давление в этих точках. Учитывая, что , ясно, что давление задается касательной к кривой  f(V) при  , а m – есть отрезок, отсекаемый этой касательной на оси ординат. Равенство давлений имеет место, если касательные параллельны. Это условие можно осуществить большим числом способов, если бы не равенство химических потенциалов, т.е. касательные должны совпадать, а это возможно единственным способом. Фазовое равновесие возможно только между такими состояниями вещества (жидкости и пара), которым отвечают точки касания этой прямой с кривойf(V). Аргументы этих точек устанавливают изменение удельного объема вещества при его переходе из жидкого 1 в парообразное состояние 2, величину равновесного давления  и химического потенциала  (при заданной температуре T). Построение Максвелла, которое мы обсудили, позволяет сделать важный прогноз относительно величины . Ему отвечает «полочка Максвелла», соединяющая на изотерме жидкое и парообразное состояния. О высоте полочки можно получить определенные сведения, если известно уравнение состояния, описывающее  на изотерме (например, уравнение состояния газа Ван-дер-Ваальса). Поскольку эти уравнения аналитические, их можно экстраполировать в межфазную область, в которой равновесное состояние невозможно, так как 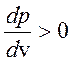. Петля Ван-дер-Ваальса сшивает устойчивые ветви изотермы с 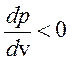. Очевидно, что «полочка» лежит в промежутке между максимумом и минимумом на этой «петле», но эта неопределенность несовместима с однозначным определением равновесия. И действительно, из равенств (265) и (266) имеем:

                                           (267)

но

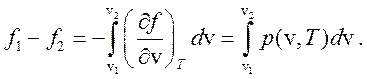                                        (268)

 Сравнивая выражения (267) и (268) имеем

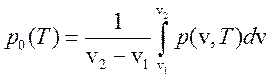                                                        (269)

и , т. е. величина скачка удельных объемов определяется правилом Максвелла ( равенство площадей 1 и 2 на рис. 22).

                  

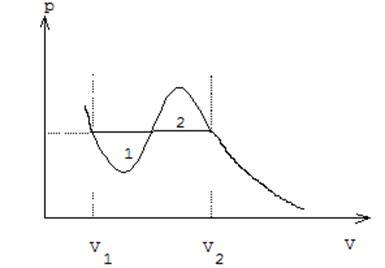
              Рис. 22. Правило Максвелла на pV-диаграмме

В свою очередь изобара на TS-плоскости (для газа Ван-дер-Ваальса) имеет вид, показанный на рис. 23. Покажем, что положение изотермы равновесия, определяющее скачок удельной энтропии,  удовлетворяет      тому    же    правилу     Максвелла (т. е. равенство площадей 1 и 2). Действительно, из выражений (265) и (250) имеем:

                                                                                       (270)

 и

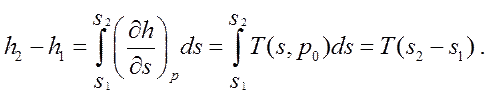                   (271)

                      

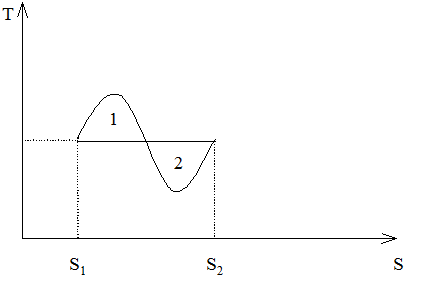
                Рис. 23. Правило Максвелла на TS-плоскости