Тримолекулярные реакции. Учет нарушения равновесного распределения. Теория Линдемана

В п. 1 показано, что для реакции между атомами  можно найти из соотношения

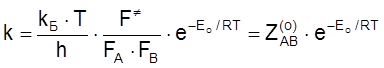                        ,        (4.47)

т. е.

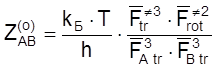                                      .                       (4.48)

Полагая (при грубых оценочных расчетах) величины F_i для одинаковых степеней свободы разных частиц по порядку величины одинаковыми, получаем из соотношения (4.48), что

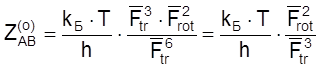                             .             (4.49)

При обычных (не слишком высоких) температурах типичными для статсумм являются значения

 см^–1,                ,                            .

Подставляя в формулу (4.46) выражение (4.49) для  и выражения типа (4.43) или (4.44) для статсумм активированного комплекса и исходных молекул, можно оценить значения стерического фактора f для бимолекулярных реакций между молекулами разного типа.

Случай 1. Реакция между атомом A и n-атомной линейной молекулой B, идущая через линейный активированный комплекс:

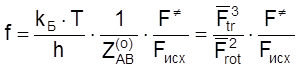                               .               (4.50)

Для  и  имеем

,

.

Отсюда

.

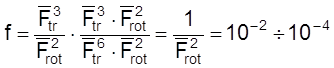Случай 2. Реакция между атомом A и n-атомной линейной молекулой, идущая через нелинейный активированный комплекс.

Для  и  имеем

,

,

.

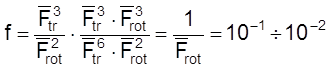Случай 3. Реакция между атомом и нелинейной n-атомной молекулой. Активированный комплекс в этом случае нелинейный.

Для  и  имеем

;                        .

Тогда

.

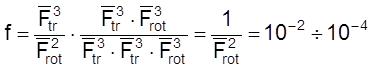Случай 4. Реакция между двумя линейными молекулами, идущая через линейный активированный комплекс.

Для  и  имеем

;                     .

Тогда

.

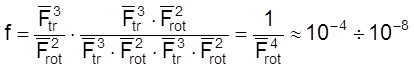Случай 5. Реакция между двумя линейными молекулами, идущая через нелинейный активированный комплекс. В этом случае

.

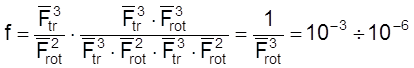Случай 6. Реакция между линейной и нелинейной молекулами. В этом случае активиро­ванный комплекс нелинейный и

.

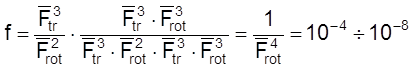Случай 7. Реакция между двумя нелинейными молекулами. В этом случае активирован­ный комплекс нелинейный и

.

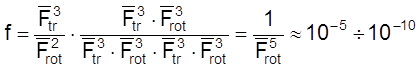Как видим, значения стерического фактора могут изменяться от  для реакции между атомами до  для реакций между нелинейными много­атомными молекулами. Интервал  перекрывает практически весь диапазон значений f, который до сих пор удавалось наблюдать экспериментально. В этом согласии с экспериментом – большой успех теории активированного комплекса.

До сих пор наши расчеты f носили грубо оценочный характер. Однако, рассматривая конкретные реакции и задаваясь для них конкретной структурой активированного комплекса, можно оценивать значения f со значительно большей точностью. Все же, учитывая приближенный характер теории активированного комплекса и отсутствие достаточно надежных данных о структуре активированного комплекса, вряд ли стоит требовать от этой теории большего, чем предсказание порядка величины предэкспоненциального множителя  и стерического фактора f.

4.5.2. Тримолекулярные реакции

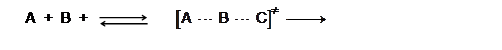Теория активированного комплекса позволяет легко вычислить число тройных столкновений. Для безактивационной реакции (т. е. реакции с ) между тремя атомами

А + B + C      [A … В … C]^¹       P,

имеем

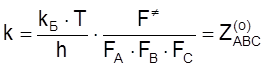                                  ,                  (4.51)

где  – фактор тройных столкновений, т. е. число тройных столкновений в единице объема в единицу времени при единичных концентрациях частиц A, B и C.

Общее число тройных столкновений в единице объема в единицу времени

.

Используя приближенные величины ,  и , для фактора тройных соударений имеем

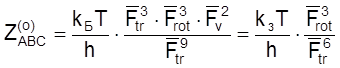                            .           (4.52)

Учтем, что при

,

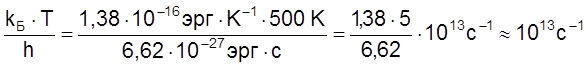а

.

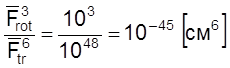(Мы рассматриваем для определенности столкновения малых молекул, поэтому принимаем значение , т. е. равное нижней границе типичного интервала для .) Тогда получаем, что

.

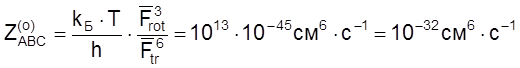Это значение  в пределах точности оценок совпадает с нормальным значением пр­е­д­­экспо­нен­циального множителя для тримолекулярных реакций  cм⁶ × c^–1, оцененного нами в п. 3 разд. 2.1.4 из простейших соображений.

Стерический фактор для тримолекулярных реакций между частицами различного строения можно оценить тем же способом, что и для бимолекулярных реакций:

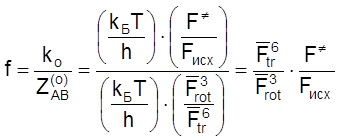                            .             (4.53)

Например, для реакции между тремя нелинейными молекулами:

.

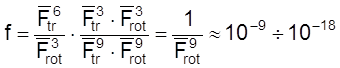Для реакции между двумя атомами и многоатомной нелинейной молекулой:

.

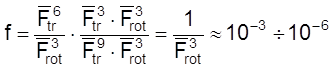Для реакции между двумя атомами и двухатомной молекулой, протекающей через линейный активированный комплекс:

.

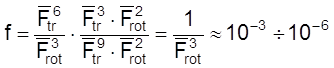Вероятность тройных столкновений мала, поэтому в газовой фазе тримолеку­ляр­ные реакции обычно играют существенную роль только в тех случаях, когда их энергия активации равна нулю или мала. Примером важной тримолеку­ляр­ной реакции является рекомбинация атомов A и B:

в присутствии третьей частицы M. Роль M состоит в отводе энергии от AB, благодаря чему молекула AB не диссоциирует назад на атомы A и B.

В жидкой фазе, где концентрации реагентов могут быть более высокими, чем в газах, тримолекулярные реакции более вероятны.

4.5.3. Мономолекулярные реакции

Мономолекулярные реакции очень распространены, особенно при высоких температурах. К ним относятся реакции распада и изомеризации молекул, свободных радикалов и ионов.