Синтез сигналов по Фурье (лабораторная работа)

Министерство образования Российской Федерации

Рыбинская государственная авиационная технологическая академия имени  П. А. Соловьева

Кафедра радиоэлектронных и телекоммуникационных систем

КИРИЛЛИН А. Н.

Синтез  сигналов  по  фурье

Методические указания

к лабораторной работе по дисциплине

"Основы радиоэлектроники и связи"

Рыбинск

2003

Цель работы – изучение возможности аппроксимации сигнала многочленом Фурье по ортогональной системе гармонических функций.

Синтезируются периодические сигналы различной формы и сигналы с амплитудной и угловой модуляциями. Исследуется влияние числа ортогональных составляющих на погрешность аппроксимации.

2.1 Краткие теоретические сведения

Как отмечалось в первой лабораторной работе, для синтеза сигналов в качестве базисной системы можно использовать систему ортогональных функций . Аппроксимация сигнала  конечным числом членов обобщенного ряда Фурье

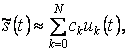                                                                                  (2.1)

где 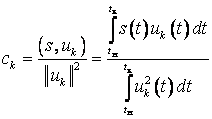 – коэффициент обобщенного ряда Фурье

обеспечивает наилучшее приближение в смысле минимума среднеквадратической ошибки:

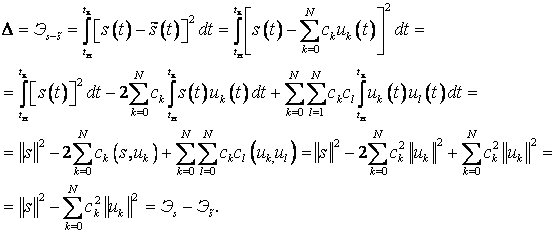(2.2)

Из этого выражения видно, что среднеквадратическая ошибка – это энергия разностного сигнала . Она может быть определена как разность энергий сигнала  и аппроксимирующей функции .

Относительная среднеквадратичная погрешность аппроксимации

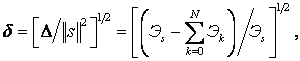                                                (2.3)

где – энергия k-ой составляющей сигнала.

Для сигналов, имеющих бесконечную энергию, но конечную мощность, среднеквадратическая ошибка определяется в смысле мощности. Например, периодические сигналы с конечной мощностью имеют бесконечную энергию, так как определены на интервале времени .

Очевидно, что при увеличении числа слагаемых в (2.1) среднеквадратическая ошибка уменьшается. Если ортогональная система функций является полной (ее нельзя дополнить функцией, ортогональной всем функциям системы), то с увеличением числа слагаемых среднеквадратическую ошибку можно сделать сколь угодно малой.

Как указывалось в первой лабораторной работе, из множества систем ортогональных функций в радиотехнике широкое применение нашли гармонические функции. Они являются периодическими, поэтому используются для синтеза периодических видеосигналов:

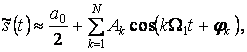                                                           (2.4)

где  – амплитуда k-ой гармоники;

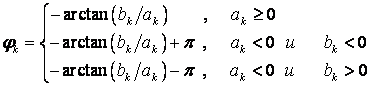– начальная фаза гармоники;

;

;

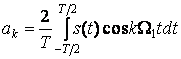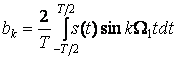– частота основной (первой) гармоники сигнала;

Т – период сигнала.

Учитывая, что мощность постоянной составляющей сигнала , а мощность k-ой гармонической составляющей , относительная среднеквадратичная погрешность аппроксимации