Теория линейных колебаний. Свободные колебания, страница 4

2. Существует абсолютный максимум . Достигается он при . Точное значение резонансной частоты можно получить исследуя максимум резонансной кривой – рис. n7. Ей соответствует минимум подкоренного выражения в (20). Дифференцируя подкоренное выражение и приравнивая производную к нулю получаем точное значение резонансной частоты: . В пределе малого затухания , . При частоте вынуждающей силы, равной собственной частоте осциллятора наступает резонанс. Как видно, коэффициент передачи в этом случае наибольший, причем равен добротности осциллирующей системы. А добротность тем выше, чем меньше затухание.

3. В пределе больших частот  Коэффициент передачи стремится к нулю  по закону .

Замечание. В пределе малых частот  постоянная вынуждающая сила задает дополнительное постоянное смещение – амплитуда колебаний стремится к величине отклонения, которое было бы под действием постоянной силы. .

При резонансе амплитуда колебаний в  раз больше, чем .

      Используя общие свойства комплексного числа, представим комплексную амплитуду в виде: . Реальная и мнимая части определяются:

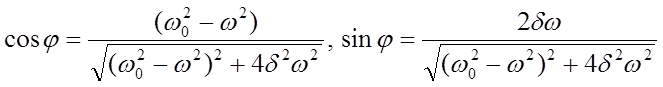        (21)

Окончательно, полное решение уравнения колебаний (16) имеет вид:

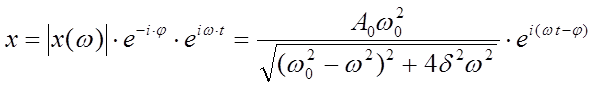        (22)

Амплитуда вынужденных колебаний прямо пропорциональна амплитуде внешней силы .

Из выражения (22) следует, что смещение отстает по фазе от вынуждающей силы на угол ,  тангенс которого определяется из:

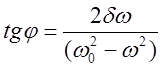                          (23)

При стремлении  к нулю . Угол  из области положительных значений.

С ростом  и приближением частоты к собственной частоте осциллятора , вблизи резонанса , следовательно .

При переходе через т.   скачком достигает бесконечных отрицательных значений .

В пределе  , следовательно . График функции приведен на рис. n9.

      Из комплексного вида решения можно выделить, например, его действительную часть. Тогда, общий вид представим формулой:

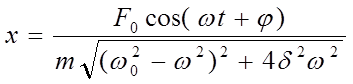
В резонансе:

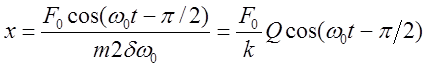
Скорость колеблющегося тела можно получить дифференцированием приведенных выражений:

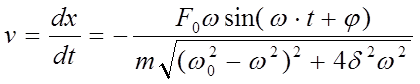
В резонансе:

.

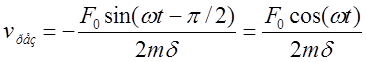Умножая  на  убеждаемся, что при резонансе вынуждающая сила равна силе трения. Отметим, что сдвиг фазы между скоростью и силой равен нулю.

      Интересно убедиться, что амплитуда скорости установившихся вынужденных колебаний определяется выражением:

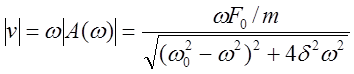
Легко видеть, что эта величина достигает максимума при . Наступает резонанс скорости. Из уравнения (23) видно, что сдвиг фазы между смещением и вынуждающей силой  при  достигает . Всегда между смещением и скоростью имеется точно такой – же сдвиг. Следовательно, при резонансе скорости внешняя сила и скорость совпадают по фазе. Другими словами сила в произвольный момент времени действует в направлении скорости, работа внешней силы положительна и идет на преодоление сил трения.

      Замечания относительно превращения энергии при вынужденных колебаниях. Полная мгновенная величина энергии осциллятора при произвольной частоте:

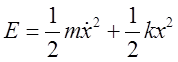
меняется со временем в течение периода. Внешняя сила совершает работу, компенсируя потери энергии из-за силы трения лишь за период.

      При низких частотах средняя за период кинетическая энергия гораздо меньше средней потенциальной, т.к. мала скорость тела. При высоких частотах напротив, кинетическая существенно больше потенциальной. В резонансе - при совпадении частот внешней силы и собственной частоты осциллятора, средние за период кинетическая и потенциальная энергии сравниваются.