Сферическая аберрация. Решение задачи о преломлении света на центрированной сферической поверхности

ЛЕКЦИЯ

Сферическая аберрация

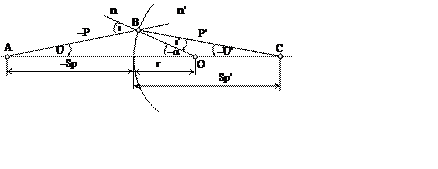Рассмотрим точное решение задачи о преломлении света на центрированной сферической поверхности (центр кривизны лежит на оптической оси).  Введем правило знаков для углов и отрезков. Угол будем считать положительным если поворот от луча к оси происходит по часовой стрелке (чтобы правило знаков было аналогичным правилу знаков в матричной Гауссовой оптике). За начало координат примем точку пересечения сферической поверхности с оптической осью. Рассчитаем площади ΔABO и ΔBCO двумя способами.

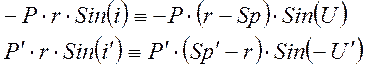                                                        (1)

Учтя закон Снелиуса – nSin(i)=n^/Sin(i^/), получим уравнение:

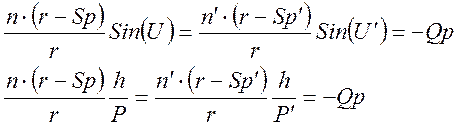                                                        (2)

Эти уравнения называются инвариантом Аббе (h – расстояние от оптической оси до пересечения луча со сферой или высота луча). В параксиальном приближении Sp=P=S, и (2) переходит в соотношение называемое нуль инвариантом.

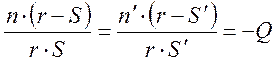                                                        (3)

Из (3) очевидна известная из параксиальной оптики формула для преломления света на сферической поверхности:

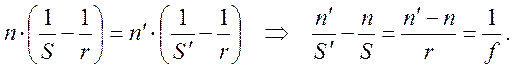                                                        (4)

Рассмотрим отображение точки в точку широкоугольными пучками. Исключим из инварианта Аббе (2) величины P и P^/, воспользовавшись теоремой косинусов:

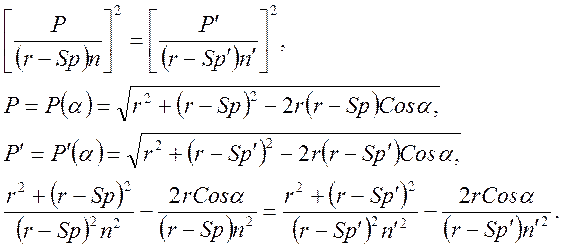                                          (5)

Поскольку, по условию, зависимости от угла быть не должно, в (5) должны быть равны между собой отдельные слагаемые.

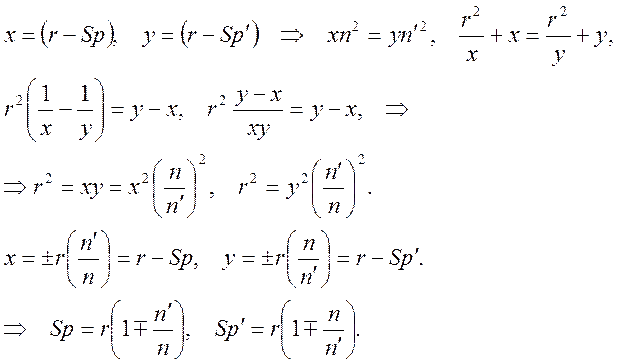                     (6)

Смысл формул (6) в том, что пучок лучей, вышедший из точки отстоящей от преломляющей поверхности, на расстоянии Sp, соберется в сопряженной точке на расстоянии от преломляющей поверхности Sp^/независимо от величины телесного угла, содержащего пучок лучей (или высот пучка лучей). Эти сопряженные точки, связанные стигматическим отображением, называются апланатическими. Помимо точек, удовлетворяющих условиям (6) (знак ± в формулах (6) следует принять +, при знаке – выполняется равенство  Qp=– Qp’) уравнения (5) допускают еще несколько решений:

                                      (7)

Первое равенство отвечает случаю, когда предмет и изображение находятся на преломляющей сферической поверхности. При этом пучок лучей, выходящий из точки на поверхности, остается гомоцентрическим. Во втором случае все лучи пучка ортогональны поверхности и не преломляются, и пучок не искажается и также остается гомоцентрическим. Комбинируя эти апланатические точки для двух поверхностей толстой линзы, можно получать апланатические толстые линзы.

Рассмотрим искажения гомоцентрического пучка лучей сферической поверхностью в общем случае в первом неисчезающем приближении. Напишем величину обратную инварианту Аббе, в которой расстояние P разложим до квадрата угла α:

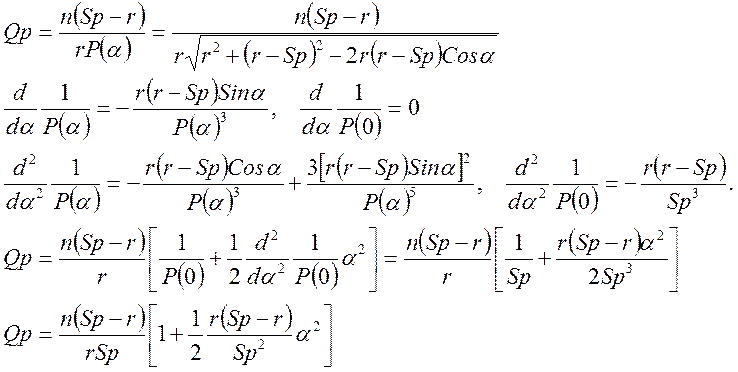                     (8)

Будем считать, что Sp=S+δS, где S –расстояние в параксиальном приближении, δS – продольная сферическая аберрация. В силу цилиндрической симметрии δS пропорциональна четным степеням угла U (U^/) между лучом и оптической осью. Разложим (8) по степеням δS:

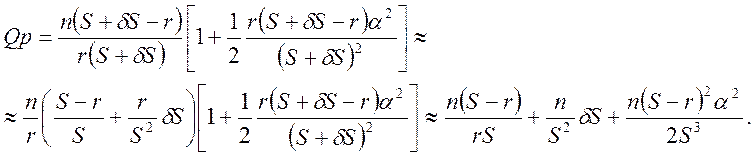                     (9)

Приравняем разложение инварианта Аббе для входного и выходного лучей:

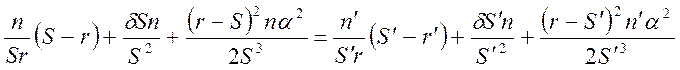                   (10)

Первые слагаемые в (10) можно сократить – это параксиальные нуль-инварианты. Выделяя из оставшихся частей (10) нуль-инварианты, выражению (10) можно придать вид:

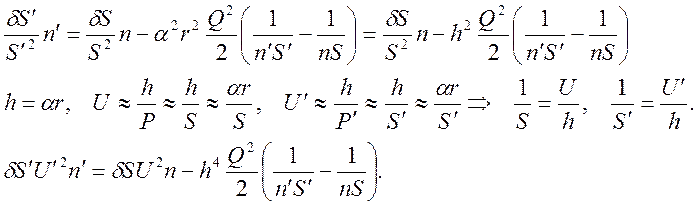                   (11)

Соотношение (11) можно применить для системы центрированных сферических поверхностей. Производя суммирование правых и левых частей уравнений и сокращение одинаковых слагаемых в правой и левой части, получим окончательное выражение для продольной сферической аберрации центрированной оптической системы:

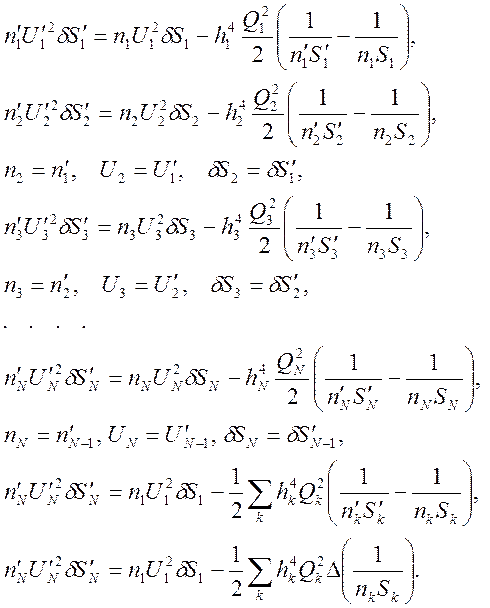                                      (12)

Поскольку продольная сферическая аберрация возникает при отклонении углов U_k от параксиальных углов, то можно связать δS_k c U_k. из-за аксиальной симметрии минимальный порядок разложения δS_k квадратичный по углам U_k.

Тогда выражение для сферической аберрации принимает вид: 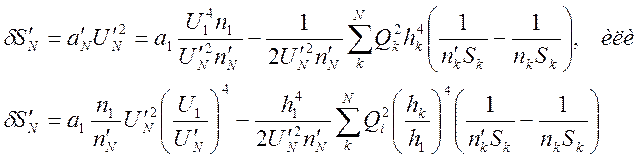                   (13)

В формуле (13) первое слагаемое  обращается в ноль, если предмет безаберрационный (a₁=0), если предмет лежит на бесконечности (U₁=0). Выражение со знаком суммы называется первой суммой Зайделя. В (13) первая сумма Зайделя выражена через высоты луча. Заменой переменных ее можно выразить через углы (в форме Ланге):

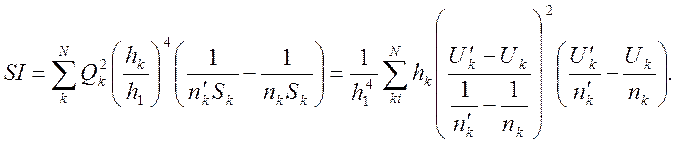                    (14)

Рассмотрим примеры сферической аберрации. Для случая одной преломляющей поверхности формула (13) примет вид:

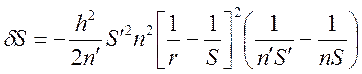                                      (15)

Легко видеть, что условия обращения в ноль сферической аберрации совпадают с условиями апланатизма. В данном случае результаты приближенных расчетов совпали с точными. Для сферического зеркала в среде с показателем преломления n нужно положить n’=-n.

Для тонкой линзы в воздухе первая сумма Зайделя состоит из двух слагаемых (n₁=n₂^/=1, n₂=n₁^/=n, S₂=S₁^/, h_i=h₁=h) имеет вид:

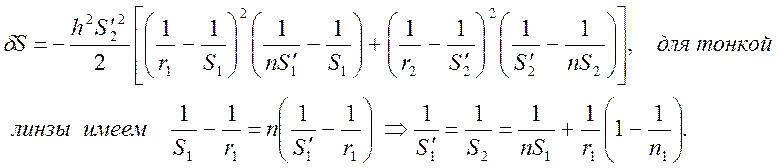                   (16)

Введем обратные величины 1/f=φ, 1/S₁=σ, 1/r₁=ρ, 1/S₂^/=1/S₁+1/f=σ+φ. Тогда величина в (16) в квадратных скобках ([…]=A) запишется следующим образом:

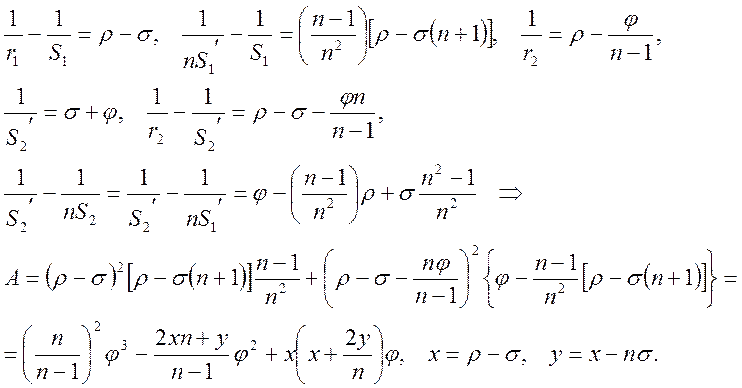                   (17)

Если предмет находится на бесконечности (σ=0, x=y=ρ) то формула (17) упрощается:

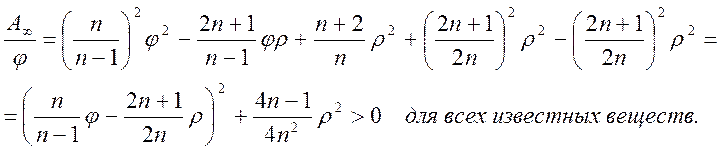                   (18)

Величина продольной аберрации зависит от типа линзы. Для собирающей линзы продольная аберрация отрицательна, а для рассеивающей - положительна. Найдем параметры линзы наиболее благоприятной формы с минимальной продольной аберрацией при фиксированном фокусном расстоянии. Для этого продифференцируем выражение (18) по ρ и приравняем производную нулю:

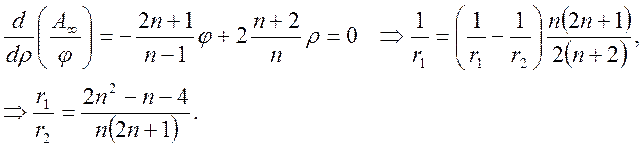                   (19)

Легко убедиться, что для стекла n=1.5 соотношение радиусов кривизны r₁/r₂=‑1/6, т.е. линза двояко выпуклая. Радиус, на который падает свет из бесконечности, меньше в 6 раз выходного радиуса тонкой линзы.