Сегнетоэлектрики. Регистрация петли гистерезиса, страница 3

Следствием доменной структуры сегнетоэлектрика является гистерезисная зависимость P(E). Полный дипольный момент кристалла определяется суммой моментов доменов. Поэтому в отсутствие внешнего поля поляризация доменов скомпенсирована и для образца в целом равна нулю. При включении поля E, достаточно слабого для того, чтобы переориентировать диполи, направленные против поля, кристалл ведет себя как линейный диэлектрик (участок oa на рис. 3). При дальнейшем увеличении напряженности поля полный момент образца меняется за счет смещения доменных границ, а также зарождения и роста новых доменов. В результате действия этих механизмов скорость роста P(E) увеличится (участок ab на рис. 3) и, наконец, когда весь кристалл перейдет в состояние с направлением поляризации вдоль E, наступает участок насыщения (bc), на котором рост P(E)происходит за счет индуцированной поляризации. Экстраполяция прямолинейного участка bc по линейному закону

 (9)

где P_i = Eχ − индуцированная поляризация, а χ – диэлектрическая восприимчивость, до пересечения с осью ординат дает величину спонтанной поляризации образца P_s.

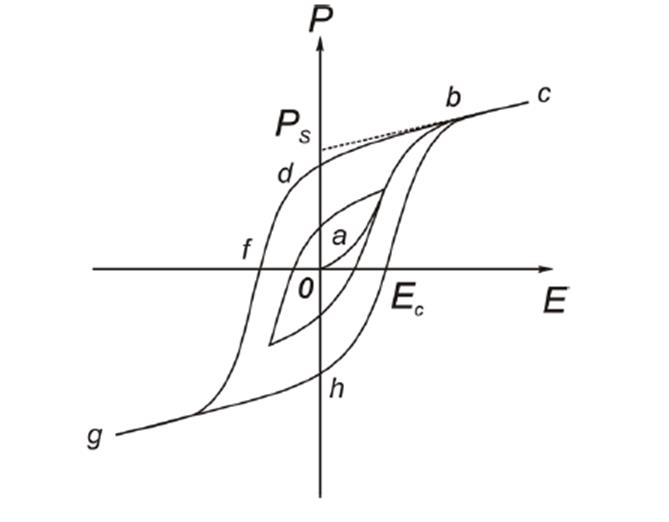
При уменьшении поля и дальнейшем увеличении обратного поля изменение P(E) идет по кривой bdfg, лежащей выше начального участка кривой, т.к. смещение доменных границ и рост новых доменов задерживается. При полном цикле изменения поля в прямом и  обратном направлении кривая описывает замкнутую петлю гистерезиса. Поле E_с, которое надо приложить для того, чтобы уменьшить P до нуля называется коэрцитивным полем. Величина коэрцитивного поля в сегнетоэлектриках зависит от таких факторов, как температура, частота поля, толщина образца и качество кристалла. Величина поляризации P_r на обратной кривой при E = 0 называется остаточной поляризацией. Вектор электрической индукции D определяется соотношением:

  (10)

Поэтому зависимость индукции от поля тоже имеет вид гистерезисной петли. Для сегнетоэлектриков 4πP>>E, Р>>ε₀E, поэтому зависимости P(E) и D(E) различаются только масштабом.

            Кривая oabc, которую описывает точка вершины частного цикла при плавном увеличении поля, называется основной кривой поляризации D_oabc(E). Из-за нелинейной зависимости D_oabc(E) следует различать дифференциальную диэлектрическую проницаемость:

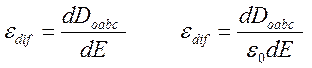(11)

и диэлектрическую проницаемость, определяемую как коэффициент наклона D_oabc(E) в начале координат

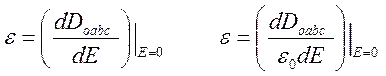 (12)

1.6 Табличные данные для BaTiO₃

Тс, К	Ps, 10-6 Кл/см2	С, К	Ec, 105 B/м	ε, в слабом поле
393	26,0 (296 K)	1,5•105	0,5 - 2 (293 К)	(8 - 10)·103 (393 K) 160 - 4000 (293 K)

2.  Эксперимент

2.1 Регистрация петли гистерезиса

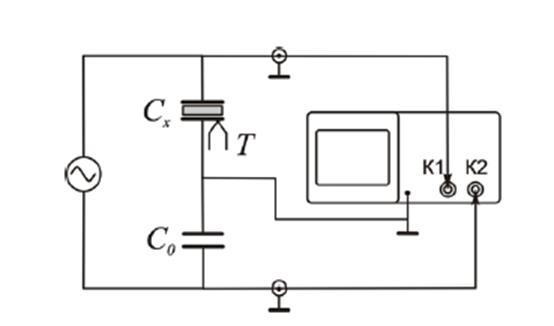
                                                 Схема установки. С_х – конденсатор с сегнетоэлектриком

                                                 С₀ – линейный конденсатор

Напряжение U_x, снимаемое с конденсатора с сегнетоэлектриком подается на вход Х осциллографа. Это напряжение пропорционально полю между обкладками конденсатора:

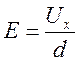 (13)

Заряды на двух последовательно соединенных конденсаторах равны, т.е. С_хU_x=C₀U_y. Кроме того из граничных условий следует, что

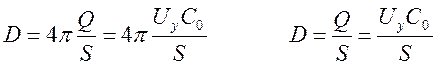 (14)

Напряжение на линейном конденсаторе пропорционально индукции, а если выполняется 4πP>>E (СГС) или P>>ε₀E (СИ), то можно записать:

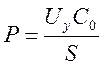 (СИ) (15)

3.  Результаты

3.1 Петля гистерезиса предельного цикла

P_s=35 ± 2 мКл/м²­

P_r=21 ± 2 мКл/м²

E_c=40 ± 5 кВ/м

Потеря энергии на переполяризацию

~1мкДж

3.2 Построение ε_dif(E) и определение ε

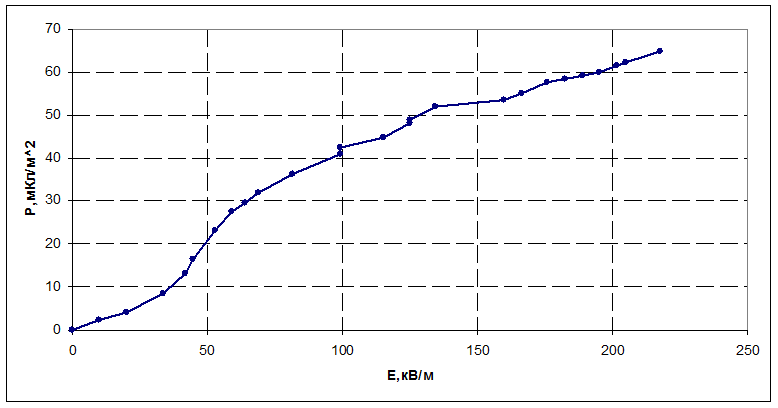
ε ~ 4000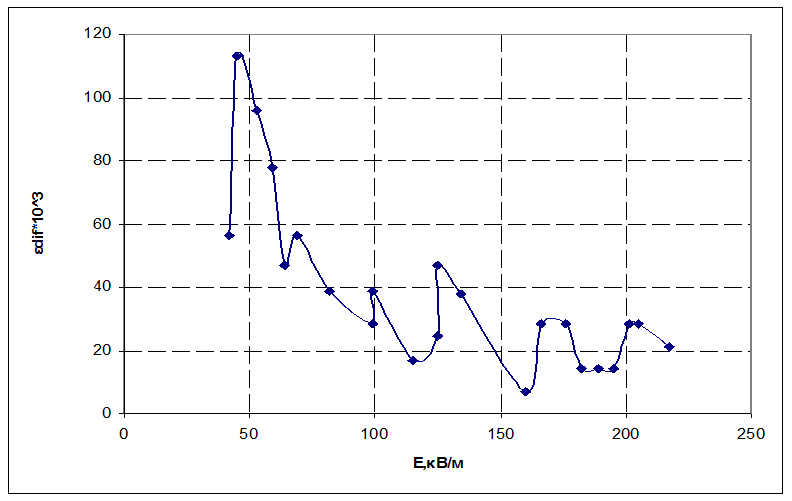            

3.3 Определение температурной зависимости спонтанной поляризации и температуры перехода

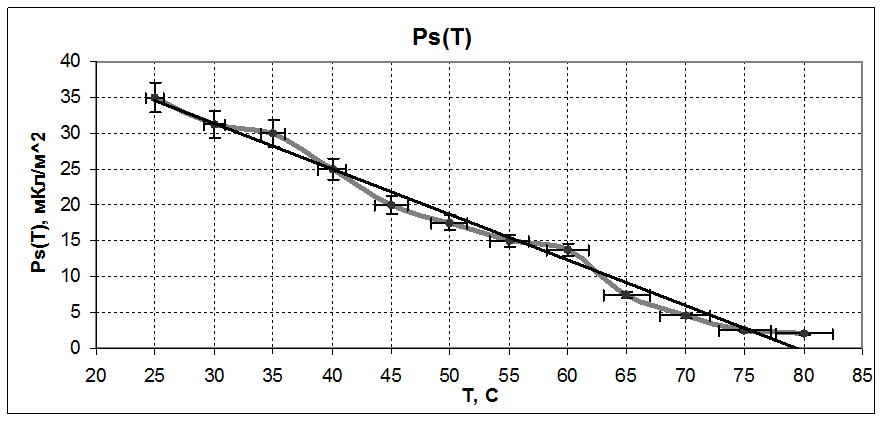
T_c = 80 ± 5 ‘C

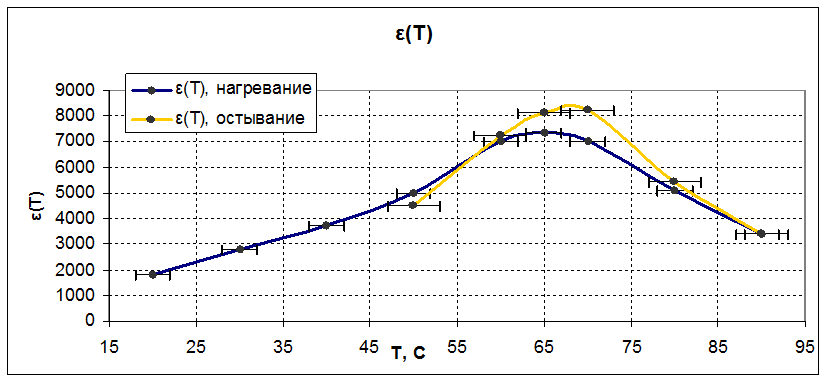3.4 Определение температурной зависимости диэлектрической проницаемости ε(Т) Проверка закона Кюри-Вейсса в области фазового перехода

ε(T) = C_x(T)/C

C = ε₀S/d

T_c = 67 ± 5 ‘C

Пусть в точке фазового перехода ε принимает конечное значение ε_с, тогда в обобщенном виде закон Кюри-Вейсса запишется в виде:

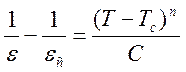 (17)

Логарифмируя это выражение, получим:

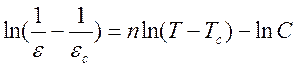 (18)

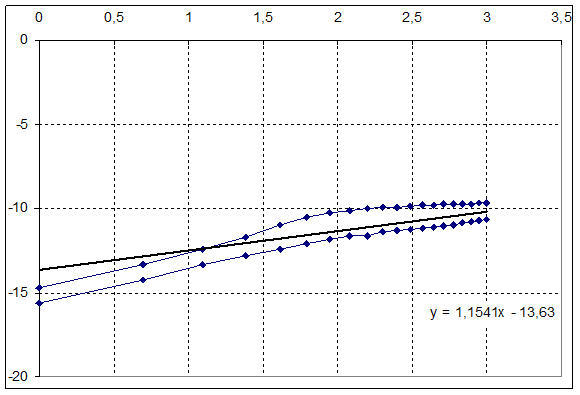n = 1,15

C = exp(13,63) = 8,3•10⁵