Пользуясь стандартными электродными потенциалами, рассчитайте стандартное изменение энергии Гиббса DG0 и сделайте вывод о возможности самопроизвольного протекания процесса:
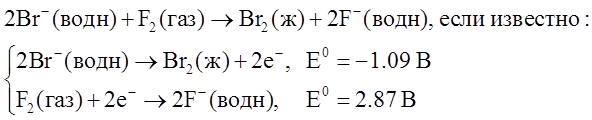
Решение:
Складывая две полуреакции, получаем, что для данной реакции E0=1.78 В. Отсюда, учитывая, что n=2, получаем: DG0 = -nFE0 = -344 кДж/моль. Реакция идёт самопроизвольно.
При каких температурах начнётся процесс конденсации воды из водяного пара при его давлении 1 атм, если образуются капельки воды размером 100Å. s=0.0728 Дж/м2, DHисп = 40.66 кДж/моль.
Решение:
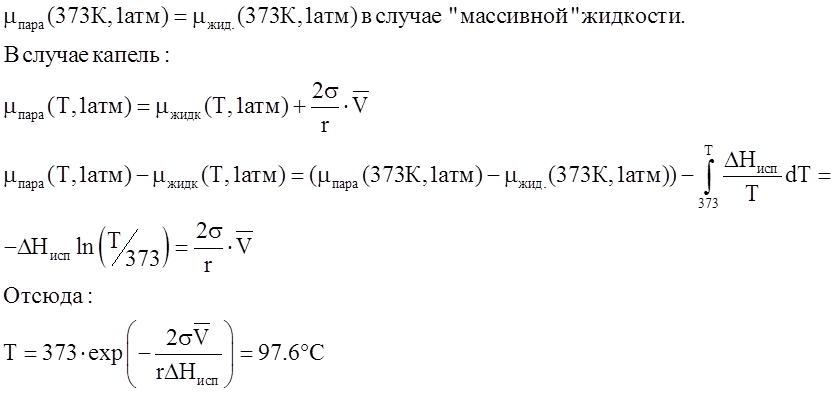
Найти зависимость эффективной мольной теплоёмкости 
от температуры для 1 моля смеси
орто- (спин 1) и пара- (спин 0) водорода. Известно, что при переходе молекулы
водорода из орто- в пара- состояние выделяется DH0=-1.418 кДж/моль тепла.
Решение:
Cv молекулы водорода 7/2.
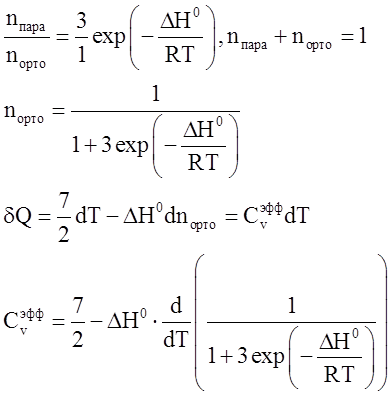
Задача 4. (90 баллов). Известно, что наиболее частой причиной «перегорания» лампы накаливания является истоньшение нити до ее плавления. Оцените минимально возможную толщину вольфрамовой нити в лампе накаливания, если ее температура составляет 3000 К. Удельная теплота плавления вольфрама составляет 191 кДж/кг, температура плавления – 3416 К, плотность при 3000 К ρ = 18.6 г/см3, атомный вес MW = 183.86. Избыточную поверхностную энергию вольфрама считать равной 4 Дж/м2
Решение:
ln (T/Tп) = – (1* Vтвs)/(ΔH r)
(за использование «2» снимать 20 б. или м.б. наоборот – за «1» добавлять 20 б.)
Vтв = M/ ρ = 9.9 10-6 м3
Δ Н = 35 кДж/моль
ln(T/Tп) = – 0,13
r = 10-9*4/3.5/0.13 = 8,8 10-9 м
d = 1,76.10-8 м = 17,6 нм
Задача 5. (90 баллов) Равновесная степень покрытия поверхности металлического никеля атомарным водородом вследствие адсорбции водорода на Ni0 из чистого водорода при температуре 298 К, давлении 1 атм составляет около 0,95. Оцените равновесную степень покрытия поверхности металлического никеля водородом при обработке частиц металлического никеля смесью 10 % об. Н2 – 90 % об. N2
Решение 19 = θ1/{(1-θ1)P11/2} = Кадс = θ/{(1-θ)P1/2}
θ/{(1-θ) = 6
θ = 0,86
Задача 6. (дополнительная, 120 баллов при условии, что в сумме не более 400) В 10—3 М раствор FeCl2 при 25оС опустили железный и хлор-серебрянный электроды. Оцените ЭДС элемента (Fe|FeCl2,AgClçAg). Опишите равновесное состояние системы. Стандартные электродные потенциалы составляют
хлор-серебряного электрода AgCl|Ag0: E0 = 0,222 В отн. НВЭ,
железного электрода: Fe2+|Fe0: E0 = – 0,44 В отн. НВЭ
Fe3+|Fe2+: E0 = 0,77 В отн. НВЭ
Решение
2AgCl + Fe0 ó 2Ag0+Fe2++2Cl-
ЭДС = Ехс-Еж = 0.222 – (–0.44) – RT/(2F)(2 ln aCl- + ln aFe2+) = т.к. x(Cl-) = 2x(Fe2+)
= 0.662 – 3/2 RT/F(ln aFe2+) – (RT/F)ln2= 0,662 + 0,0385*2,3*2 – 0.0178 В = 0,822 В
(за это 40 баллов)
Учет Д-Х дает ln γ+ = -1.179*4*(0.025)1/2 = - 0.75
ln γ- = -1.179*(0.025)1/2 = - 0.19
Поправка к ЭДС составит
DE = – RT/(2F)(2 ln γCl- + ln γFe2+) = + 0,0128 * 1,12 В= 0,014 В
Ответ ЭДС = 0,834 В (за это – уже 80 баллов)
Равновесие 3 ln aFe2+ = 6,9 lg aFe2+ = 1.324 F/RT = 51, то есть при aFe2+ > 10 7, т.е. никогда, пока есть Ag+.
В равновесии, весь 2AgCl + Fe0à 2Ag0+Fe2++2Cl-, пока не кончится AgCl, либо Fe0
(за это – полный балл - 120 баллов)
В зависимости от того, что кончилось раньше, так же необходимо рассмотреть
либо равновесие
3 Fe2+ ó2 Fe3+ + Fe0 (DG = 1.98 F = 191 kJ/mol) – реакция практически не идет
либо равновесие AgCl + Fe2+ óAg0+Fe3++Cl-
ЭДС = Ехс-Еж-ж = 0.222 – (0.77) – RT/(F)( ln aCl- + ln aFe3+/ aFe2+) =
= - 0.548 – 0,0128 (ln aCl- + ln aFe3+/ aFe2+)
~ – 0,370 – 0,0128 (ln aFe3+/ aFe2+) = 0
ln (aFe3+/ aFe2+) = – 29, то есть реакция опять таки практически не идет.
То есть в равновесии Fe 3+ в системе практически не будет.
(за это – особый бонус - 140 баллов)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.