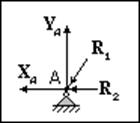
 рассмотреть условия равновесия узла А, находящегося под действием сил ХА,
YA (получены на стадии определения внешних реакций) и неизвестных
сил R1, R2 (реакции со стороны разрезанных стержней)
рассмотреть условия равновесия узла А, находящегося под действием сил ХА,
YA (получены на стадии определения внешних реакций) и неизвестных
сил R1, R2 (реакции со стороны разрезанных стержней)
В этом случае мы имеем систему сходящихся сил, для которой можно записать два условия равновесия: суммы проекций сил на оси X и Y должны быть равны нулю. Из этих двух уравнений можно будет найти неизвестные силы R1 и R2. Если после проведения вычислений окажется, что силы R1 и R2 имеют отрицательные значения, то это просто означает, что соответствующие стержни не сжаты, а растянуты.
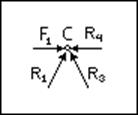 Следующим
объектом, равновесие которого мы рассмотрим, будет узел С. Мысленно вырезаем
узел С и рассматриваем его равновесие под действием внешней силы F1
и реакций разрезанных стержней R1, R3 и R4.
Опять имеем систему сходящихся сил, две из которых известны по модулю (F1
и R1), а две требуется определить (R3 и R4) из
двух уравнения равновесия..
Следующим
объектом, равновесие которого мы рассмотрим, будет узел С. Мысленно вырезаем
узел С и рассматриваем его равновесие под действием внешней силы F1
и реакций разрезанных стержней R1, R3 и R4.
Опять имеем систему сходящихся сил, две из которых известны по модулю (F1
и R1), а две требуется определить (R3 и R4) из
двух уравнения равновесия..
Важно: мы по прежнему считаем все стержни фермы сжатыми, т.е. при рассмотрении равновесия узлов направляем реакции разрезанных стержней от стержней к узлам, но при вычислениях подставляем значения уже определенных сил с тем знаком, с каким они у нас получились.
Таким образом мы продолжаем вырезание узлов и перемещаемся по ферме. Получаем каждый раз задачу о равновесии сходящейся системы сил, не более двух из которых еще неизвестны. В правильно сконструированной ферме мы всегда будем иметь такую ситуацию, ферма не имеет "избыточной" жесткости и задача всегда является статически определимой.
б) Метод Риттера позволяет не проводя последовательных вычислений напряжений в стержнях фермы сразу получить напряжения в интересующих нас стержнях (в нашем случае пусть это будут стержни 4,5 и 6).
 Для
решения задачи мысленно разрежем ферму по сечению NN (рис. в начале параграфа).
Далее отбрасываем правую (или левую) от разреза часть и рассматриваем
оставшуюся часть конструкции как находящуюся в равновесии под действием внешних
сил и реакций с левой (правой) стороны от разреза и реакций разрезанных
стержней 4,5 и 6. В нашем примере это будет задача: конструкция из трех
стержней 1, 2 и 3 находится в равновесии по действием внешних сил F1,
F2, реакций XА, YА, а также реакций
разрезанных стержней R4, R5 и R6. Имеем
стандартную задачу на равновесие плоской системы сил, для которой мы можем
составить три уравнения равновесия (два уравнения проекций сил на оси координат
и уравнение моментов сил относительно любой точки). Эти три уравнения позволят
нам найти неизвестные силы R4, R5 и R6. Как и
в случае метода вырезания узлов в правильно спроектированной конструкции мы
всегда сможем сделать такой разрез, который пересечет не более трех стержней,
напряжение в которых требуется определить.
Для
решения задачи мысленно разрежем ферму по сечению NN (рис. в начале параграфа).
Далее отбрасываем правую (или левую) от разреза часть и рассматриваем
оставшуюся часть конструкции как находящуюся в равновесии под действием внешних
сил и реакций с левой (правой) стороны от разреза и реакций разрезанных
стержней 4,5 и 6. В нашем примере это будет задача: конструкция из трех
стержней 1, 2 и 3 находится в равновесии по действием внешних сил F1,
F2, реакций XА, YА, а также реакций
разрезанных стержней R4, R5 и R6. Имеем
стандартную задачу на равновесие плоской системы сил, для которой мы можем
составить три уравнения равновесия (два уравнения проекций сил на оси координат
и уравнение моментов сил относительно любой точки). Эти три уравнения позволят
нам найти неизвестные силы R4, R5 и R6. Как и
в случае метода вырезания узлов в правильно спроектированной конструкции мы
всегда сможем сделать такой разрез, который пересечет не более трех стержней,
напряжение в которых требуется определить.
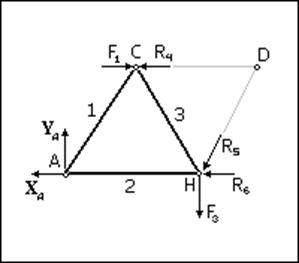
Особенностью метода Риттера является то, что мы будем рассматривать равновесие оставшейся части конструкции не в виде трех стандартных уравнений, о которых говорилось выше, а в виде альтернативного варианта условий равновесия плоской системы сил, состоящего из трех уравнений моментов сил относительно трех точек. Это так называемые точки Риттера – точки попарного пересечения стержней, напряжения в которых нужно определить.
Первой точкой Риттера будет точка D (точка пересечения стержней 4 и 5). В уравнение моментов сил относительно этой точки силы R4 и R5 не войдут (их моменты относительно этой точки равны нулю, т.к. линии действия этих сил проходят через эту точку). В уравнение для точки D войдут только силы F2, реакции XА, YА, а также неизвестная реакция разрезанного стержня R6. Искомую реакцию R6 из этого уравнения мы и определим.
Второй точкой Риттера будет точка H (точка пересечения стержней 5 и 6). В уравнение моментов сил относительно этой точки войдут только сила F1, реакция YА, а также неизвестная реакция разрезанного стержня R4. Из этого уравнения определяем R4.
Третья точка Риттера (точка пересечения стержней 4 и 6) оказывается на бесконечности (стержни 4 и 6 параллельны). Поэтому вместо уравнения моментов для такого случая нужно записать уравнение проекций сил на направление, перпендикулярное параллельным стержням (в нашем случае это уравнение проекций на ось Y). В это уравнение силы XA, F1, R4 и R6 не войдут (а войдут только силы YA, F2 и R5) и мы будем иметь уравнение для определения неизвестного напряжения в стержне 5 - силы R5.
§ 1.8. Распределенные силы
Интенсивность q распределенной силы – это сила, приходящаяся на единицу объема, поверхности или длины линии. Чаще встречаются параллельные и сходящиеся распределенные силы.
Рассмотрим линейные распределенные силы (по линии) на отрезке.
|
|
а)
АВ=l |
|
|
б)
|
|
|
в)
АВ=l; Точку приложения равнодействующей вычислим через определение момента элементарных сосредоточенных сил |
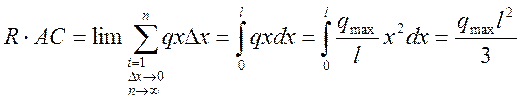
А так как 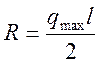 , то
, то 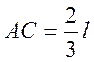 , то есть равнодействующая проходит через
центр масс эпюры распределенных сил.
, то есть равнодействующая проходит через
центр масс эпюры распределенных сил.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.