Для нахождения вероятностей перехода между колебательными состояниями используется принцип Франка – Кондона, который в своей классической формулировке утверждает, что при переходе молекулы из одного электронного состояния в другое не происходит заметного изменения ни относительного положения, ни относительных скоростей атомных ядер. Этот принцип основан на том обстоятельстве, что за время изменения электронного состояния (т.е. перестройки электронной оболочки) ни геометрия молекулы, ни скорости ядер не успевают заметно изменится. Впервые это утверждение сформулировал Франк в рамках классической механики. Более строгий подход был реализован в рамках квантовой механики Кондоном. Принцип Франка Кондона в современной трактовке есть метод расчета вероятностей перехода между колебательными состояниями. Такие вероятности (факторы Франка – Кондона) для многих молекул рассчитаны и затабулированы.
 Структура молекулярных спектров. Совокупность переходов между двумя электронными
состояниями
Структура молекулярных спектров. Совокупность переходов между двумя электронными
состояниями ![]() образуют ряд полос, соответствующих
переходам между двумя колебательными состояниями
образуют ряд полос, соответствующих
переходам между двумя колебательными состояниями ![]() .
Частоты электронных полос лежат обычно в ультрафиолетовой или оптической
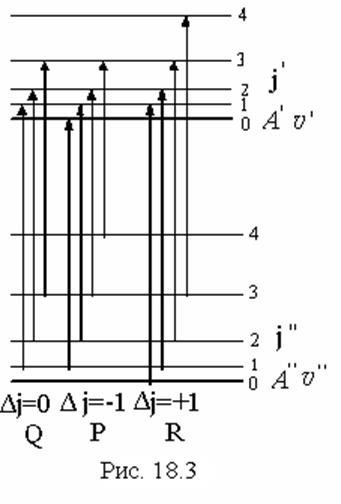
области. На рис 18.2 показаны переходы между различными колебательными
состояниями двух электронных уровней. На рис. 18.3 выделена одна полоса
.
Частоты электронных полос лежат обычно в ультрафиолетовой или оптической
области. На рис 18.2 показаны переходы между различными колебательными
состояниями двух электронных уровней. На рис. 18.3 выделена одна полоса ![]() . Серии линий с
. Серии линий с ![]() называются
называются
![]() ветвями. Если бы колебательные уровни были
строго эквидистантны , полосы с одинаковым
ветвями. Если бы колебательные уровни были
строго эквидистантны , полосы с одинаковым ![]() накладывались
бы друг на друга. В действительности строгой эквидистантности нет, и полосы с
одинаковым
накладывались
бы друг на друга. В действительности строгой эквидистантности нет, и полосы с
одинаковым ![]() образуют близко расположенные
последовательности полос.
образуют близко расположенные
последовательности полос.
Исследуем вращательную структуру полос
двухатомной молекулы. Частоты линий во вращательной структуре легко определить
из (18.2) и правил отбора. Для ![]() и
и ![]() ветвей получим
ветвей получим
![]() (18.3),
(18.3),
![]() (18.4),
(18.4),
![]() (18.5).
(18.5).
Здесь 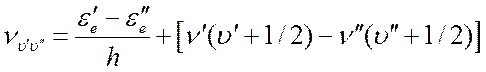 . Вращательная
структура зависит от того, какая из двух вращательных постоянных больше:
. Вращательная
структура зависит от того, какая из двух вращательных постоянных больше: ![]() или
или ![]() . В
случае
. В
случае ![]() спектр имеет низкочастотную границу, где
линии сгущаются (“красный” кант); линии простираются в сторону высоких частот,
и расстояние между ними возрастает. При
спектр имеет низкочастотную границу, где
линии сгущаются (“красный” кант); линии простираются в сторону высоких частот,
и расстояние между ними возрастает. При ![]() ,
наоборот, кант “фиолетовый” и линии простираются в сторону низких частот. При
,
наоборот, кант “фиолетовый” и линии простираются в сторону низких частот. При ![]() линии в полосе расположены равномерно.
линии в полосе расположены равномерно.
Электронные переходы в молекулах обычно
лежат в ультрафиолетовой или видимой области ![]() . В
некоторых молекулах (барий, йод) ближайший электронный уровень, на который
разрешен переход из основного состояния, лежит довольно низко, и молекула
поглощает видимый свет. Такие газы сильно окрашены.
. В
некоторых молекулах (барий, йод) ближайший электронный уровень, на который
разрешен переход из основного состояния, лежит довольно низко, и молекула
поглощает видимый свет. Такие газы сильно окрашены.
Расчет спектрального коэффициента поглощения. Молекулярные системы полос состоят из очень большого числа вращательных линий. Для детального описания такого спектра необходимы расчеты с шагом значительно меньшим ширины отдельной линии, что приводит к очень большому объему вычислений. Однако в подавляющем большинстве практически важных случаев оказывается вполне достаточным использование усредненных сечений поглощения.
Усредненное по вращательной структуре сечение поглощения (см-1 атм-1) есть [10]:
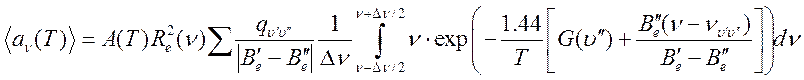 (18.6),
(18.6),
где 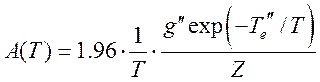 ;
; ![]() частота в
частота в ![]() ,
соответствующая центру спектрального интервала;
,
соответствующая центру спектрального интервала; ![]() температура
в
температура
в ![]() ;
; ![]() квадрат
матричного элемента дипольного момента перехода в атомных единицах;
квадрат
матричного элемента дипольного момента перехода в атомных единицах; ![]() фактор Франка-Кондона;
фактор Франка-Кондона; ![]() колебательное квантовое число и
вращательная постоянная верхнего состояния;
колебательное квантовое число и
вращательная постоянная верхнего состояния; ![]() соответственно
колебательное квантовое число, вращательная постоянная, колебательный терм,
статистический вес и энергия возбуждения нижнего уровня;
соответственно
колебательное квантовое число, вращательная постоянная, колебательный терм,
статистический вес и энергия возбуждения нижнего уровня; ![]() начало полосы;
начало полосы; ![]() статистическая
сумма молекулы. Суммирование в (18.6) проводится по тем полосам
статистическая
сумма молекулы. Суммирование в (18.6) проводится по тем полосам ![]() , для которых выполнено условие
, для которых выполнено условие ![]() .
.
Величина ![]() связана
с силой осциллятора полосы в поглощении
связана
с силой осциллятора полосы в поглощении ![]() и
временем жизни
и
временем жизни ![]() колебательного уровня
колебательного уровня ![]() соотношениями
соотношениями
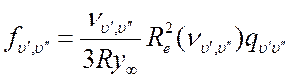 (18.7),
(18.7),
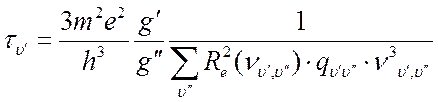 (18.8),
(18.8),
где ![]() .
.
Коэффициент поглощения есть
![]() , ( р в атм)
(18.9).
, ( р в атм)
(18.9).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.