Потенциал электрического поля приводит к изменению энергии электронов в полупроводнике создавая изгиб зон. Тут возможно несколько ситуаций: обогащение, обеднение и инверсия.
Согласно законам статистики полупроводников, если в глубине полупроводника концентрация электронов n0, то вблизи поверхности концентрация будет определяться изгибом зон:
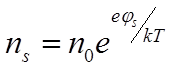 8.1
8.1
где js – изгиб зон, связанный с тем, что поверхностные состояния заряжаясь, создают потенциал. Если этот потенциал таков, что основные носители заряда притягиваются в приповерхностную зону, это называется обогащением. Если основные носители заряда отталкиваются зарядом поверхности, их концентрация вблизи поверхности меньше чем в глубине полупроводника, реализуется ситуация обеднения. Возможна ситуация, когда изгиб зон настолько велик, что вблизи поверхности происходит инверсия типа проводимости. Скажем, объемный полупроводник n- типа, а в результате инверсии, приповерхностный его слой обладает p- типом проводимости.
На рисунке 8.2 приведена ситуация обеднения концентрации электронов на поверхности, видно что вблизи поверхности полупроводник n типа становится почти собственным полупроводником.
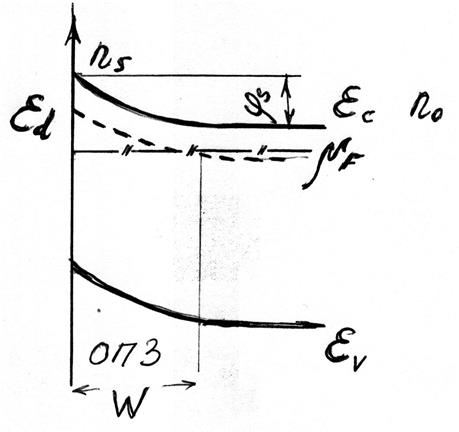
Рисунок 8.2. Иллюстрация изгиба зон (ситуация обеднения).
Простейший для анализа случай – обеднение. Решая уравнение Пуассона, можно найти распределение электрического поля и потенциала в области пространственного заряда.
Рассмотрим, как спадает напряженность электрического поля вглубь полупроводника. Из курса электродинамики известна связь между потенциалом j и объемной плотностью заряда r (уравнение Пуассона):
![]()
Обратим внимание, что в случае неоднородного электрического поля, вклад в объемную плотность заряда r* вносят и связанные заряды. Связанные электроны и ядра поляризуются, создавая дипольный момент. Вклад связанных зарядов заключается в том, что полупроводник обладает отличной от единицы статической диэлектрической проницаемостью e. Так как задача одномерна, то:
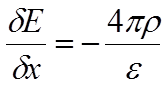
Объемная плотность заряда создается электронами, дырками, положительно заряженными донорными примесями (которые отдали электрон), и отрицательно заряженными акцепторными примесями (которые захватили электрон). То есть:
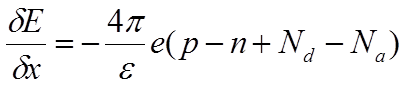 8.2
8.2
Рассмотрим случай полупроводника n-типа. Пусть концентрация доноров в глубине (далеко от поверхности) остается еще много больше концентрации свободных электронов, то есть примесь далека от истощения и уровень Ферми лежит несколько выше энергии доноров. Пусть поверхностные состояния являются акцепторными, то есть поверхность захватывает электроны из объема полупроводника, и, зарядившись отрицательно, создает потенциальный барьер js для электронов. Концентрация электронов к поверхности уменьшается, концентрация дырок растет, но не превышает концентрации электронов (не реализуется ситуация инверсии). Тогда уравнение 7.2 существенно упрощается. Концентрация дырок и электронов у поверхности близка к собственной концентрации, и, таки образом, на много порядков меньше концентрации доноров. Акцепторы нами преднамеренно не вводились, и их концентрация равна нулю (конечно в реальном полупроводнике всегда есть фоновые примеси акцепторного типа, но их концентрация мала по сравнению с концентрацией преднамеренно введённых доноров - скажем 1016 см-3 для германия, кремния либо арсенида галлия), и ими можно пренебречь. Значит, объемная плотность заряда обусловлена, в основном положительным зарядом доноров (с которых ушли электроны). На энергетической диаграмме это те доноры, энергетический уровень которых находятся выше уровня Ферми (рисунок 8.2). Предположим также, что концентрация доноров не зависит от координаты (полупроводник легирован однородно).
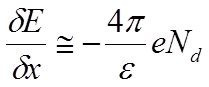
Решение тривиально, напряженность электрического поля в пределах ОПЗ изменяется линейно, и, в соответствии с граничными условиями для потенциала:
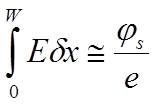
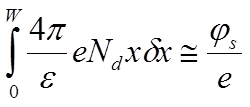
Отсюда размер ОПЗ W и максимальная напряженность электрического поля (вблизи границы) равны:
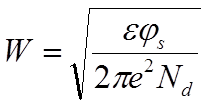
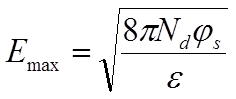 8.3
8.3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.