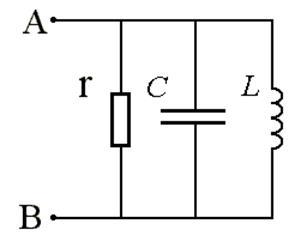
Параллельный колебательный контур. Параллельный контур в общем виде

Параллельный колебательный контур.

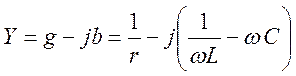  -  при 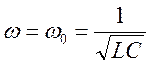 проводимость вещественная

аналогично последовательному контуру с   :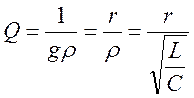

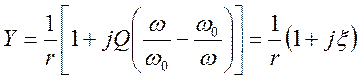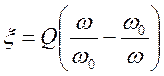      ,      - как для последовательного контура с заменой сопротивлений проводимостями, токов - напряжениями, напряжений - токами (дуальная цепь) => при резонансе  минимален и равен  , при питании от генератора тока напряжение на контуре максимально, а в контуре циркулирует большой колебательный ток - в Q раз больший, чем ток источника (перераспределение энергии C и L ) - т.н. резонанс токов.

На частоте ниже резонансной  характер проводимости (сопротивления) индуктивный (активно-индуктивный), выше   - емкостной (активно-емкостной).

Конечное внутреннее сопротивление источника  подключается  и шунтирует контур, снижая добротность до 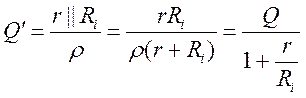   - т.е. для сохранения добротности необходим источник с  .

------------------------------------------------------------------------------------------------------

Параллельный контур в общем виде.

      

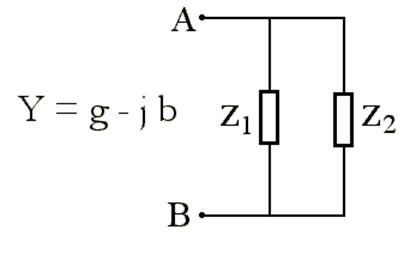
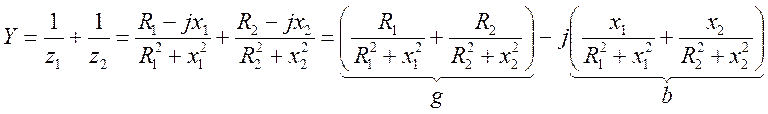
При резонансе   -   т.е.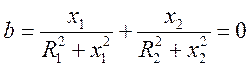      

- при этом  - резонансная проводимость.

В практически важных случаях вблизи резонанса   ,   - тогда условие резонанса 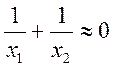     или   - в контуре с малыми потерями при резонансе реактивные сопротивления ветвей равны по величине и обратны по знаку.

При этом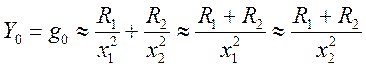   

------------------------------------------------------------------------------------------------------

Контур с потерями в L и C

  => 

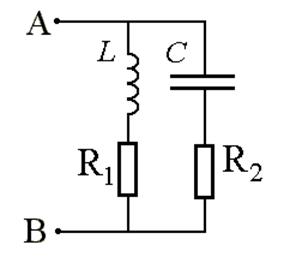
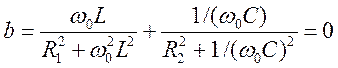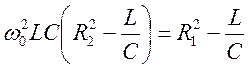
Введя 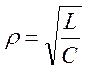    ,   находим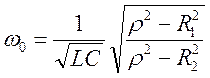

=> при           

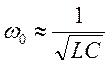
Резонансная проводимость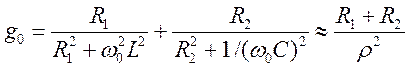  

Существенно, что при условии 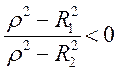   резонанса нет ни при какой   !

Кроме того :  если  -  частота  не определена ! - проводимость  вещественна при любой  - т.н. "безразличный", или "вечный" резонанс.

В общем случае при наличии резонанса  и  смещают  - за исключением случая  , когда 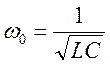  точно.

Добротность - из энергетических соотношений :

 

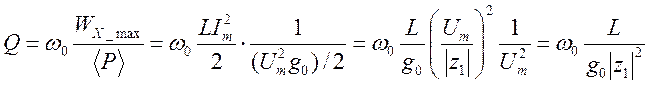
- и 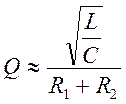   -   если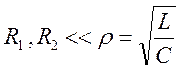  

------------------------------------------------------------------------------------------------------

Частичное включение контура

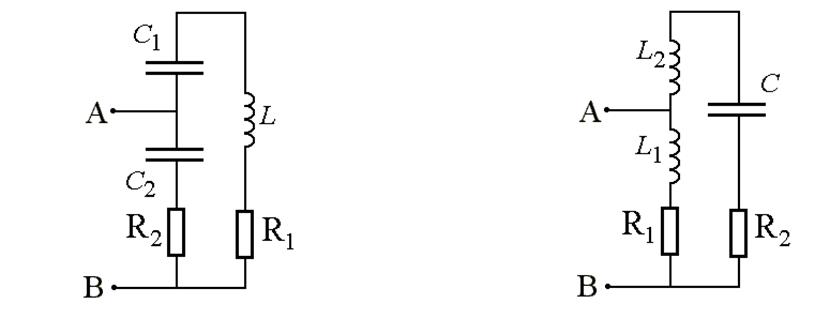
- будем рассматривать в приближении  =>  при резонансе

                         ||                  

                                                            ||

                      ||                    

                                                            ||

                                            ||                           

                                                            ||

             ||                   

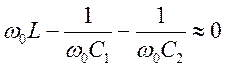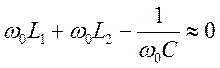
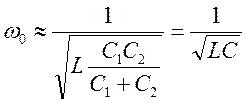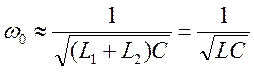
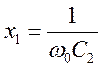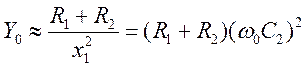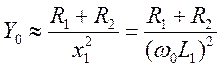
                                                       Введя :

  ,                     ||                      ,                       

                                                  

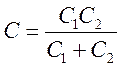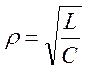
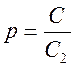               - коэффициент включения контура -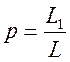      

                                                             ||

          ||              

                                                        

                                                             ||

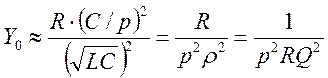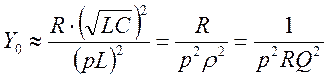
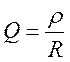
                                   -  "трансформатор" сопротивления

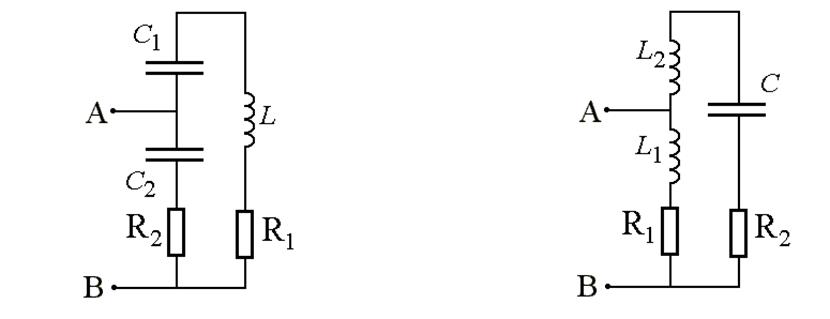
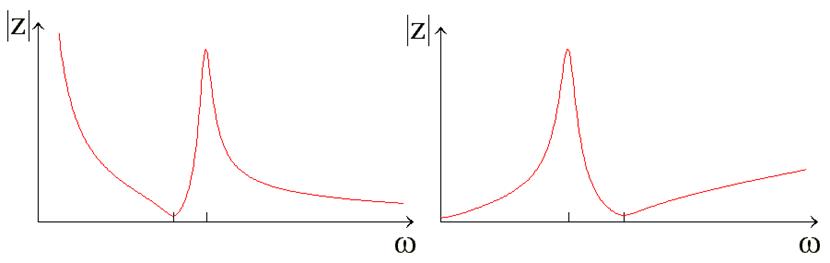
- реально в системах есть не только параллельный, но и последовательный резонанс

---------------------------------------------------------------------------------------------------

---------------------------------------------------------------------------------------------------

Связанные контура

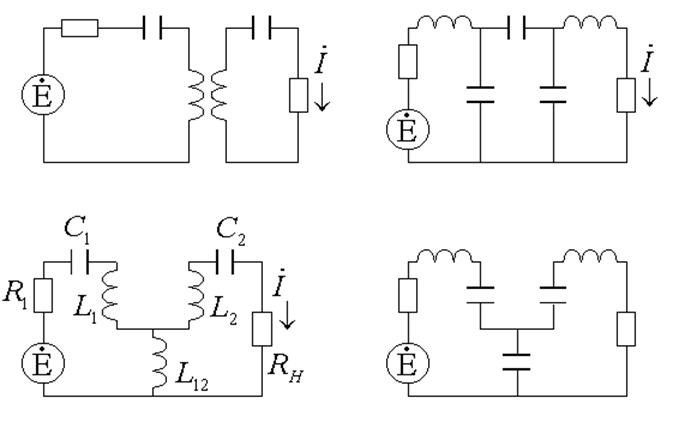
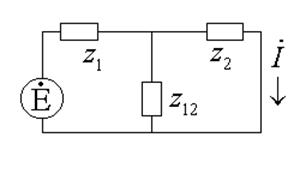
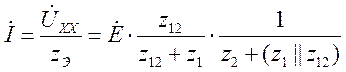
Пусть    ,   ,  

тогда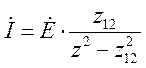  

Если     ,  то   ,      =>

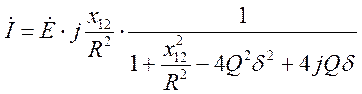
Вводят 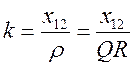  - коэффициент связи контуров =>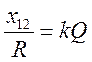 

Экстремумы тока по частоте определяются модулем знаменателя :

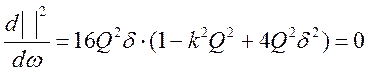
1)   

2) 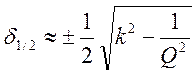        -  если  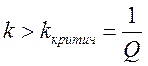, то есть еще два экстремума

                                                          

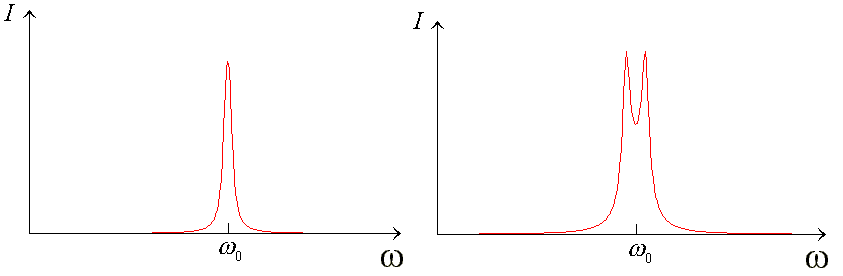
Полоса пропускания (по уровню 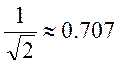) - шире, чем у одиночного контура;

для     больше в ~1.5 раза

при провале до 0.707 полоса больше в ~3 раза

------------------------------------------------------------------------------------------------------

Почему два максимума ?       Из симметрии :

                                                           

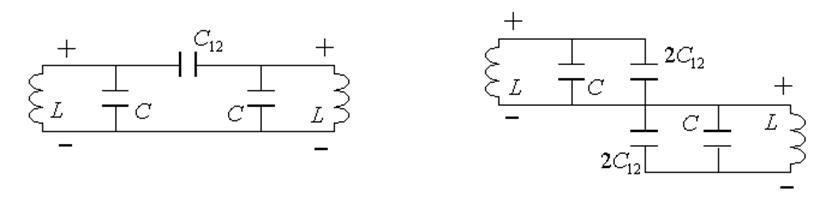
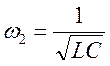
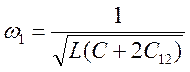
     - частоты свободных колебаний

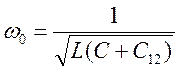        -  центральная частота