





ЛЕКЦИЯ
ПАРАКСИАЛЬНАЯ ОПТИКА. СВОЙСТВАОПТИЧЕСКИХ СИСТЕМ
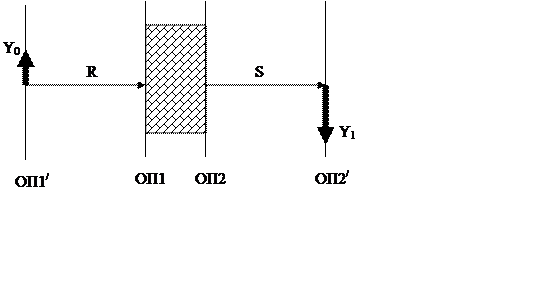
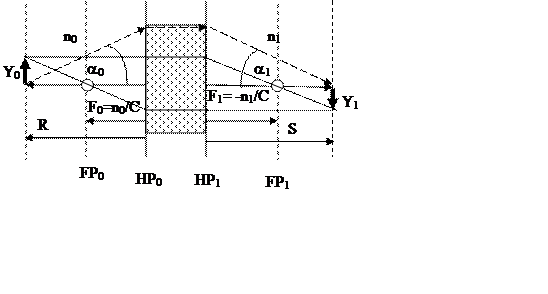
1. Экспериментальное определение элементов матрицы оптической системы. Пусть мы имеем некоторую оптическую систему, заключенную между ОП1 и ОП2. Для экспериментального определения параметров матрицы оптической системы будем помещать объекты Y0 вблизи входа в оптическую систему. На выходе из оптической системы будем искать изображения Y1.
 |
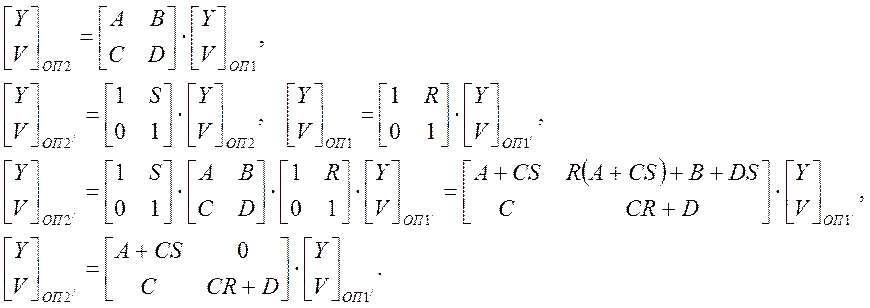 (1)
(1)
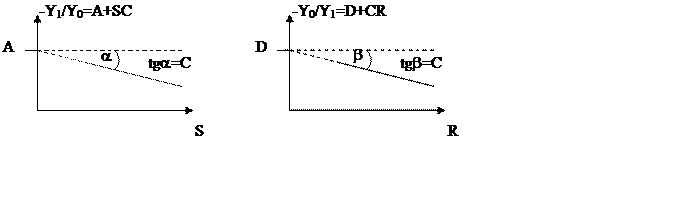 |
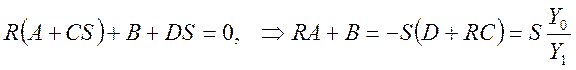 (2)
(2)
 Далее строим график зависимости
комплексной величины SY0/Y1 как функции R.
Далее строим график зависимости
комплексной величины SY0/Y1 как функции R.
Тангенс наклона дает независимое определение параметра A. Пересечение графика с осью ординат позволяют определить параметр B. Если точность измерений достаточна, должно выполняться равенство единице определителя матрицы – AD–BC=1.
2. Для построения хода лучей в оптической системе необходимо знание кардинальных точек оптической системы. Любая оптическая система имеет 6 пар кардинальных точек.
Имеется 2 фокальных плоскости. предмет, помещенный на входной фокальной плоскости, отображается на бесконечность. Предмет помещенный на бесконечность дает изображение в выходной фокальной плоскости.
Две главных плоскости оптической системы характеризуются поперечным единичным увеличением. Изображение предмета на выходной главной плоскости полностью совпадает с предметом на входной главной плоскости.
Две узловые точки лежат на оптической оси. Луч входящий во входную узловую точку под некоторым углом Θ0 выходит из выходной узловой точки под тем же углом Θ1= Θ0.
Найдем кардинальные точки произвольной оптической системы с матрицей (ABCD).
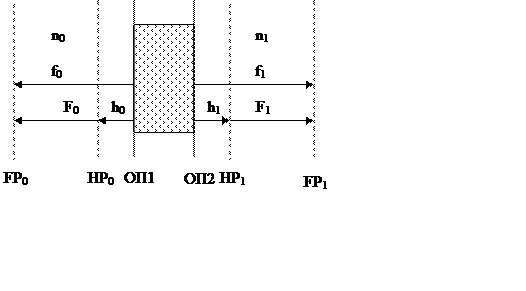
Условие, что FP0 – входная фокальная
плоскость, означает, что в преобразованной к FP0
матрице правый нижний элемент равен нулю:
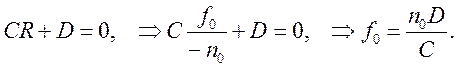 (3)
(3)
Условие, что FP1 – выходная фокальная плоскость, означает, что в преобразованной к FP1 матрице левый верхний элемент равен нулю:
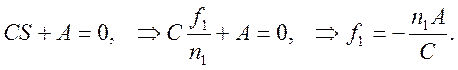 (4)
(4)
Для того, чтобы HP0 была главной входной, а HP1 главной выходной должны выполняться соотношения:
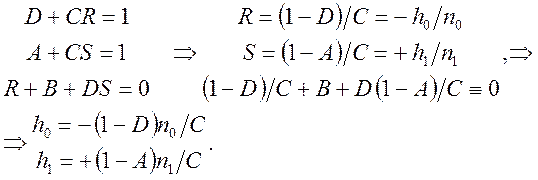 (5)
(5)
Найдем, главные фокальные отрезки F0 и F1 – расстояния от главных плоскостей до фокальных:
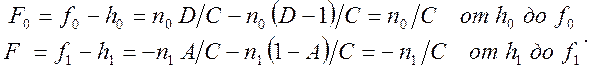 (6)
(6)
Для узловых точек u0 и u1 должно выполняться соотношение:
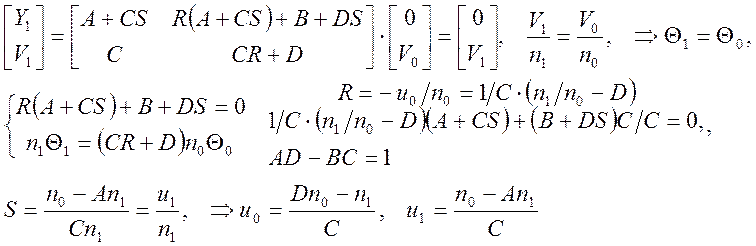 (7)
(7)
Аналогично главным фокальным отрезкам можно найти положения узловых точек, отсчитанных от главных плоскостей:
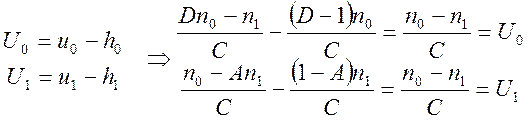 (8)
(8)
3. Приведение матрицы оптической системы к кардинальным точкам. Приведение к главным плоскостям сводится к смещению ОП1 и ОП2 в координаты отвечающие главным плоскостям. Матрица оптической системы будет очевидно иметь вид, сходный с матрицей сферической поверхности:
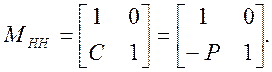 (9)
(9)
 |
Найдем матрицу оптической системы при условии, что ОП1 и ОП2 – спряженные плоскости и известна матрица оптической системы в главных плоскостях.
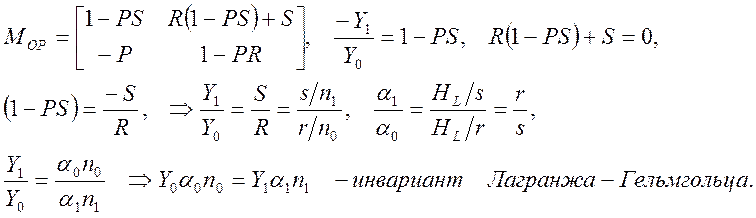 (10)
(10)
Матрица оптической системы между фокальными плоскостями имеет вид:
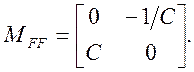 (11)
(11)
Найдем матрицу оптической системы при смещении опорных плоскостей относительно фокальных на величины Z0, Z1.
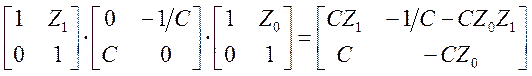 (12)
(12)
Если в точках Z0, Z1 локализованы сопряженные плоскости равенство нулю элемента матрицы В приводит к уравнению Ньютона:
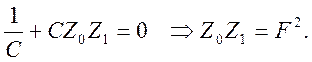 (13)
(13)
Связь между поперечным и продольным увеличением получим из (10):
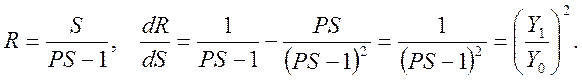 (14)
(14)


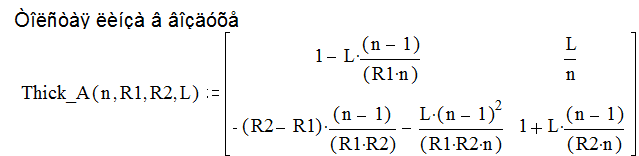



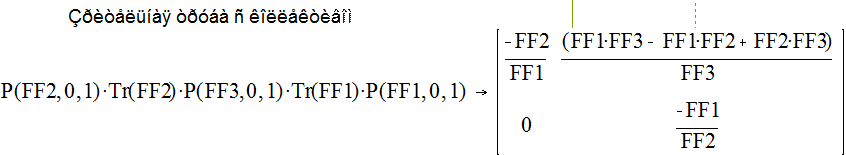


Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.