


ЛЕКЦИЯ
ПАРАКСИАЛЬНАЯ ОПТИКА. МЕТОД МАТРИЦ
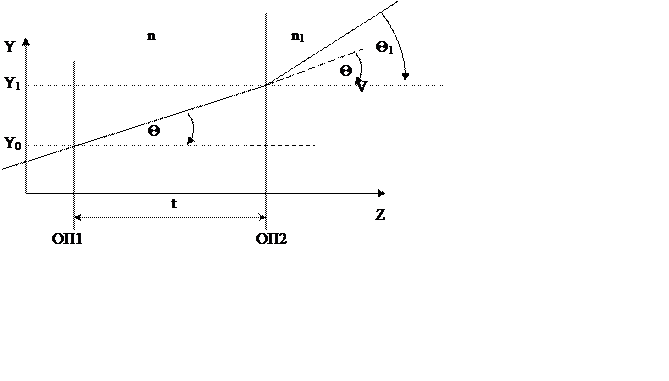
Приближение геометрической оптики λ << всех характерных размеров L. Расходимости – λ/L<<1 – все лучи – отрезки прямых линий, направление распространения которых может меняться на границе раздела двух сред с различными показателями преломления. Описание лучей – с помощью линейных функций относительно опорных плоскостей (ОП). Для описания луча в матричной оптике используются 2 параметра: высота луча – y и угол наклона к оптической оси z –Θ. Углы считаем малыми, чтобы выполнялись соотношения Θ»SinΘ»tgΘ (Θ<60) .
 |
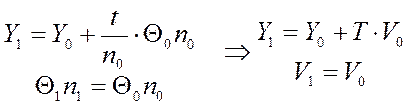 (1)
(1)
В формуле (1) сделана замена, чтобы перейти к приведенным величинам расстояний T=t/n, и углов V= Θn. Тогда конечные величины – Y1, V1 для ОП2 вычисляются через начальные – Y0, V0 (ОП1) с помощь линейного преобразования, выраженного в матричной форме:
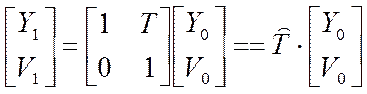 (2)
(2)
Матрица [T], относящаяся к группе унимодулярных матриц с определителем равным 1, называется матрицей перемещения. Для луча, распространяющегося в обратном направлении, угол Θ сохранит свое положительное значение , а T→–T, что достигается соглашением изменять n на –n для луча, распространяющегося в отрицательном направлении. В итоге матрица обратного перемещения будет эквивалентна обратной матрице [T]-1:
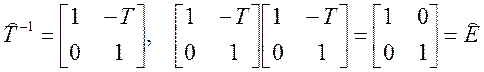 (3)
(3)
Удобство использования приведенных величин T=t/n, и V= Θn прослеживается при рассмотрении прохождения луча через границу раздела двух сред с различными показателями преломления n0 иn1. Граница раздела перпендикулярна оптической оси. Тогда на основании закона Снелиуса выполняется соотношение Θ0n0= Θ1n1 → V=V1. Считая границу раздела бесконечно тонкой, можно положить в формулах (1) t=0, что дает Y1=Y0. В итоге матрица преобразования окажется единичной - [E], Для многослойной среды матрица преобразования – это произведение матриц каждого слоя:
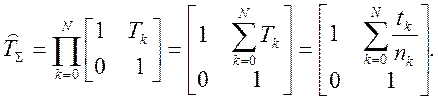 (4)
(4)
Из (4) очевидно, что направление распространения луча, прошедшего через многослойную среду определяется лишь начальным и конечным показателями преломления n0 и nN. Преобразование T=t/n также отражает экспериментальный факт кажущегося приближения предметов, находящихся в среде показателем преломления n>1 (например, в воде).
Рассмотрим прохождение луча света через сферическую границу раздела двух сред (радиус кривизны R, центр кривизны считаем лежащим на оптической оси).
Углы j
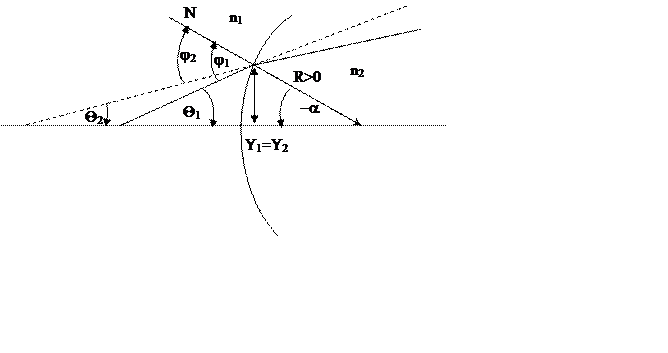 |
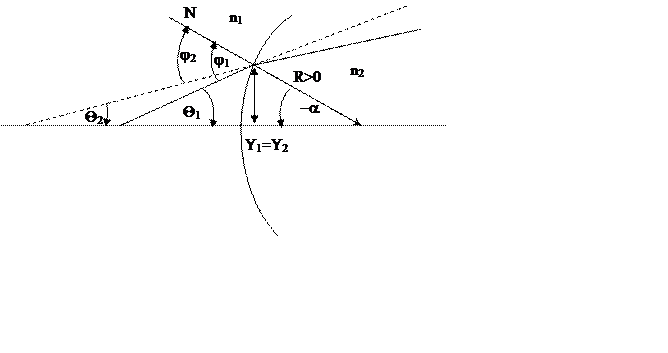 |
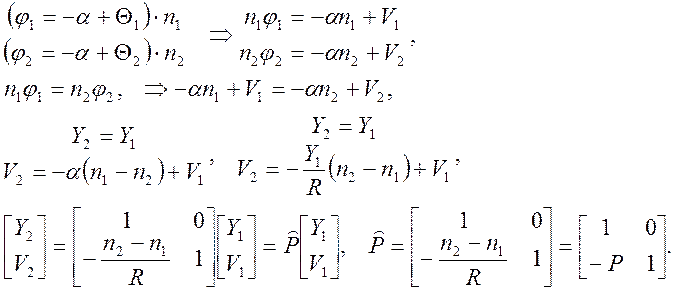 (5)
(5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.