Параксиальная оптика. Метод матриц, страница 2

Полученная унимодулярная матрица [P] – называется матрицей преломления, а величина P в левом нижнем углу называется оптической силой сферической поверхности. Определитель матрицы [P] также равен 1. Если радиус кривизны стремится к бесконечности [P]→[E] (этот результат был уже получен для преломления луча плоской границей раздела двух сред).  Если в малой области локализовано несколько сферических поверхностей, результирующая матрица преломления [P_S] – произведение элементарных матриц [P_k]. В итоге получим выражение для преобразования луча системой сферических поверхностей:

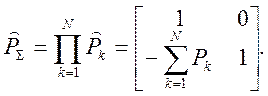                                                                                                                              (6).

Результат преобразования луча в силу коммутативности произведения (6) не зависит от порядка чередования поверхностей. Если оптическая система состоит из набора сферических поверхностей разделенных конечными промежутками, результат конечно же зависит от чередования оптических элементов, поскольку коммутативность произведения матриц преломления и перемещения отсутствует – [P]* [T]¹ [T] *[P].  В этом случае, очевидно в преобразовании луча от ОП1 к ОП2 участвует полная матрица, образованная произведениями матриц [P] и [T]: При этом определитель результирующей матрицы останется равным 1

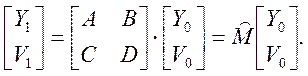                                                                                                                       (7)

При этом определитель результирующей матрицы [M] останется равным 1. Установим смысл элементов матрицы преобразования [M].

1.  Пусть оказалось, что D=0, тогда:

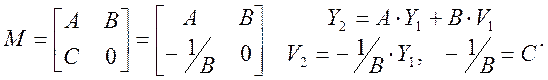
Это означает, что углы выхода лучей из ОП2 задаются лишь высотой лучей Y₁ в ОП1 и не зависят от углов лучей V₁. Т.е. все лучи, вышедшие из Y₁ будут параллельными на ОП2. Это означает, что ОП1 – входная фокальная плоскость, а B – фокусное расстояние, отсчитанное от ОП2.

2.   Пусть оказалось, что B=0, тогда:

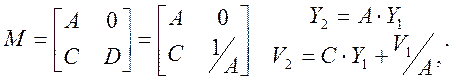
 Все лучи из точки Y₁ соберутся в Y₂ не зависимо от углов выхода. Это означает, что ОП1 и ОП2 – сопряженные плоскости (точка на ОП1 отображается в точку на ОП2). Значение параметра А отвечает поперечному увеличению.

3.  Пусть оказалось, что C=0, тогда:

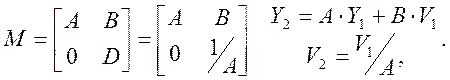
 Все лучи, имеющие углы V₁, превратятся в лучи, имеющие углы V₂. Это означает, что параллельный пучок, вошедший в ОП1 под углом Θ₁=V₁/n₁  выйдет параллельным из ОП2  под углом Θ₂=V₂/n₂, т.е. оптическая система между ОП1 и ОП2 – телескопическая с угловым увеличением  Θ₂/Θ₁= (n₁/n₂)1/A. Такая система бесконечность отображает на бесконечность. (в пункте 1 бесконечное значение B).

4.  Пусть оказалось, что A=0, тогда:

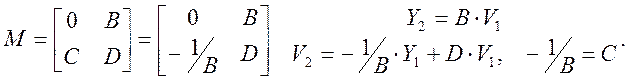
Это означает, что углы входа лучей в ОП1 задают  высоту лучей Y₂ в ОП2 и не зависят от высот лучей Y₁. Т.е. все параллельные лучи с углами V₁  на ОП1 соберутся в точку Y₂ на ОП2. Это означает, что ОП2 – задняя  фокальная плоскость, а B – фокусное расстояние, отсчитанное от ОП1.

Пусть нам известна матрица оптической системы для ОП1 и ОП2. Найдем матрицу для каких-либо  других опорных плоскостей ОП1^/ и ОП2^/, отстоящих на расстояниях S и R.

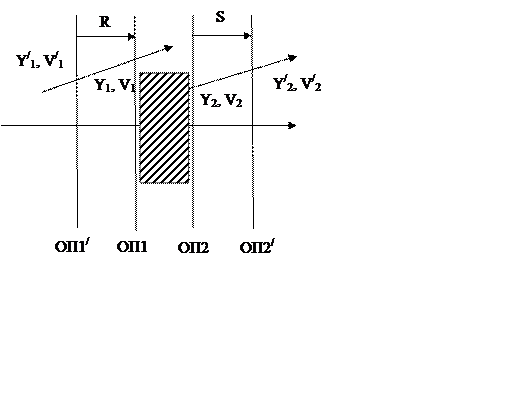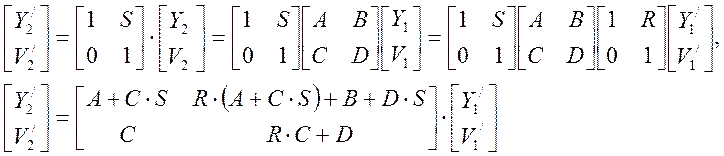                                                                                                                             (8)

Заметим, что параметр C в итоговой матрице преобразования не изменился. Согласно свойствам 1 и 4 величина –1/С  является фокусным расстоянием. Из формулы (6) легко получить известную формулу для тонкой линзы в воздухе. Т.е. матрица преобразования отвечает двум сферическим поверхностям с радиусами кривизны R₁ и R₂. Показатели преломления n₁=1, n₂=n, n₃=1.

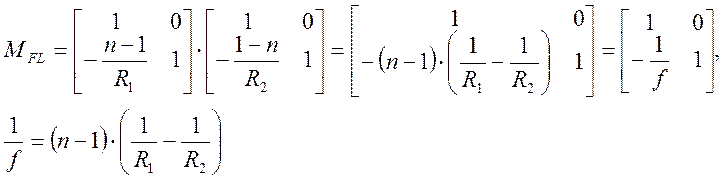                                                                                                                             (9)

Для отражения от сферического зеркала, помещенного в среду с показателем преломления  n в формуле (6) n₂=–n.

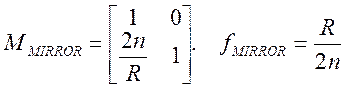                                                                                                                             (10)

Найти матрицу преобразования, отвечающую отражению от плоского зеркала отстоящего на расстоянии T: