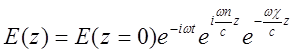 . (3.9)
. (3.9)
 Второй множитель в (3.9) с реальной
частью показателя преломления – n описывает изменение фазы волны по мере прохождения
через вещество, третий множитель, связанный с мнимой частью показателя
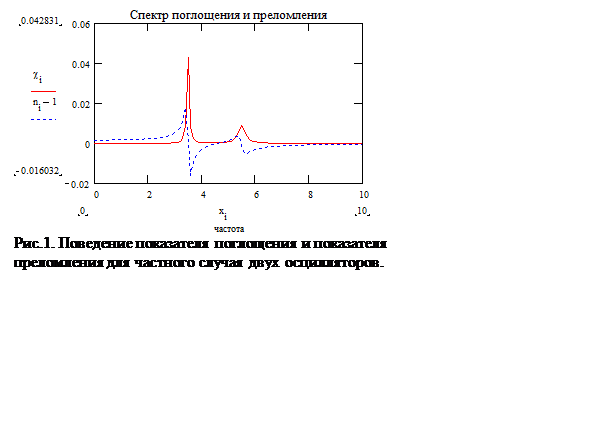
преломления задает затухание амплитуды электромагнитных колебаний. На рис.1
приведен пример спектрального поведения показателя преломления и показателя
поглощения для материала, содержащего осцилляторы двух типов: с резонансными
частотами 2.5 и 5.5.
Второй множитель в (3.9) с реальной
частью показателя преломления – n описывает изменение фазы волны по мере прохождения
через вещество, третий множитель, связанный с мнимой частью показателя
преломления задает затухание амплитуды электромагнитных колебаний. На рис.1
приведен пример спектрального поведения показателя преломления и показателя
поглощения для материала, содержащего осцилляторы двух типов: с резонансными
частотами 2.5 и 5.5.
Отчетливо прослеживаются следующие закономерности: материал прозрачен в коротковолновой, длинноволновой области спектра и вне линий поглощения. Во всех областях прозрачности наблюдается нормальная дисперсия – увеличение показателя преломления с увеличением частоты. В областях резонансного поглощения наблюдается аномальная дисперсия. Области спектра, где n-1 заметно отличается от нуля существенно шире областей спектра, поглощение заметно отличается от нуля. Эта закономерность поясняет наличие заметного показателя преломления у прозрачных оптических материалов. Она связана с различными зависимостями n(ω)-1~1/ω, χ(ω) ~1/ω2 для крыла линии. Спектр поглощения χ(ω) вблизи резонансной частоты симметричен относительно ω0, а спектральная зависимость n(ω)-1 – антисимметрична.
Поскольку в атомах составляющих оптический материал имеется много электронов, заряды ядра, то различные составляющие материала отвечают за разные участки спектра. Ядерные осцилляторы способны поглощать гамма лучи, внутренние электроны - рентгеновское излучение. за поглощение УФ излучения ответственны валентные электроны атомов и ионов. видимое излучение поглощается возбужденными электронами из основного состояния. ИК излучение поглощается из-за колебаний и вращения атомов и ионов, в том числе и из-за колебаний решетки. Ридберговские состояния и свободные электроны поглощают радиоизлучение.
Электрон в отдельном атоме обладает лишь набором дискретных значений энергий, образующих дискретный набор уровней. Спектр поглощения - узкие линии. При сближении атомов, их взаимодействие приводит к расщеплению и сдвигу уровней валентных электронов. В результате образуются широкие зоны. Глубинные электроны экранированы и их спектры искажаются гораздо слабее.
 В
зависимости от строения электронных оболочек атомов структура энергетических
зон может быть различна. На рис.2 приведены энергетический структуры
материалов разных типов, которые определяют оптические свойства этих
материалов. Проследим их на примере нормального отражения. Коэффициент
отражения по мощности R определяется формулами Френеля:
В
зависимости от строения электронных оболочек атомов структура энергетических
зон может быть различна. На рис.2 приведены энергетический структуры
материалов разных типов, которые определяют оптические свойства этих
материалов. Проследим их на примере нормального отражения. Коэффициент
отражения по мощности R определяется формулами Френеля:
|
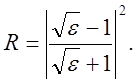 (3.10)
(3.10)
Возможно рассмотрение следующих случаев:
1. Идеальный диэлектрик σ=0. Диэлектрическая проницаемость ε чисто вещественная величина. В формуле (3.5) это отвечает затуханию γ=0. В зависимости от частоты ε может быть как положительной, так и отрицательной. При ε>0 показатель преломления вещественен и коэффициент нормального отражения R=(n-1)2/(n+1)2 <1. Процесс отражения качественно различен для ε>1, когда в силу граничных условий, сохранения тангенциальной составляющей D, на границе минимум амплитуды стоячей волны. При 0<ε<1, амплитудный коэффициент отражения меньше нуля и на границе отражения максимум амплитуды стоячей волны. Прошедшая волна проходит через среду без изменения амплитуды.
2. При ε<0показатель преломления чисто мнимый и волна через оптическую среду не проходит (амплитуда экспоненциально убывает с ростом z без изменения фазы), а коэффициент отражения по интенсивности строго равен единице.
3. В поглощающей среде σ≠0 отражение меньше единицы, и прошедшая волна испытывает затухание в среде в соответствии с инкрементом затухания.
4. Идеальный проводник отвечает случаю σ=∞. При этом отражение полное и свет в материал не проникает. Отражение возникает за счет наведенных токов свободных электронов, гасящих волну внутри материала и генерирующих отраженную волну
5. Условие ε=0 для металлов (резонансные частоты равны 0) дает условие прозрачности и определяет частотную границу зоны прозрачности – плазменную частоту:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.