




Кафедра физической химии
Определение термодинамических и геометрических характеристик двухатомных молекул из колебательно-вращательных спектров
Выполнили: А.Е.Арзамасцев
Новосибирск, 2005
Развитие методов статистической термодинамики позволяет рассчитывать термодинамические функции через суммы по состояниям. Расчётные методы имеют преимущество перед экспериментальными, так как не требуют ни высоких температур, ни высоких давлений.
Молекулы всегда (кроме температуры абсолютного нуля) находятся в тепловом движении и при соударениях постоянно обмениваются энергией. Возникает динамическое распределение по всем возможным энергетическим состояниям. Для равновесных условий оно подчиняется статистическому закону распределения Больцмана (1):
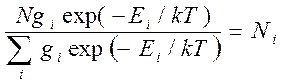 .
.
Введение статистической суммы Z позволяет описывать состояние системы из N эквивалентных частиц через набор состояний одной частицы. Это даёт возможность рассчитать некоторые термодинамические величины.
Статистическая сумма равна общему числу состояний, в которых может находиться система при данной температуре (2).
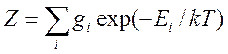
Энергия молекулы
может быть представлена как сумма поступательной и внутренней энергий, причём
последняя объединяет энергию вращения, энергию колебаний и электронную энергию:![]() . Статистическая сумма Z при этом представима в виде
. Статистическая сумма Z при этом представима в виде ![]() . Для случая N неразличимых невзаимодействующих молекул можно
выразить Z через статистическую сумму одной
молекулы Z1:
. Для случая N неразличимых невзаимодействующих молекул можно
выразить Z через статистическую сумму одной
молекулы Z1:
![]()
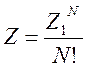 .
.
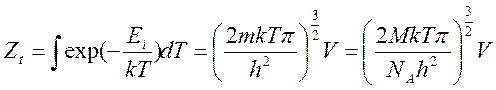 –
поступательная статистическая сумма;
–
поступательная статистическая сумма;
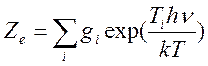 –
электронная статистическая сумма;
–
электронная статистическая сумма;
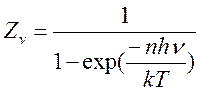 –
колебательная статистическая сумма;
–
колебательная статистическая сумма;
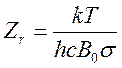 –
вращательная статистическая сумма;
–
вращательная статистическая сумма;
Со статистическими
суммами связаны основные термодинамические функции, например: 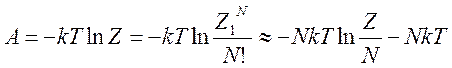 – свободная энергия, или энергия
Гельмгольца.
– свободная энергия, или энергия
Гельмгольца.
Для вычисления A через аппарат статистических сумм величину свободной энергии представляют как сумму нескольких составляющих:
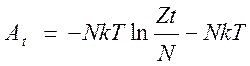 ,
, ![]() ,
, ![]() . Аналогичные выражения получены для
энтропии, энтальпии, энергии Гиббса, теплоёмкости.
. Аналогичные выражения получены для
энтропии, энтальпии, энергии Гиббса, теплоёмкости.
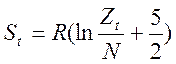 ,
, ![]()
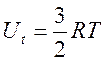 ,
, ![]() для линейных молекул (
для линейных молекул (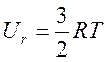 для
молекул, строение которых отличается от линейного).
для
молекул, строение которых отличается от линейного).
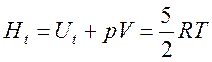 ,
, ![]() .
.
![]() ,
, ![]() .
.
Несколько более
сложно получается теплоёмкость: 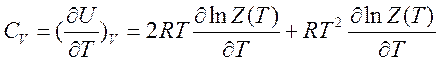 .
.
Если все состояния
системы не вырождены, то наиболее заселены состояния с низкими энергиями,
причём максимально заселено состояние E0. По мере повышения температуры возрастает относительная заселённость
состояний с более высокими значениями Ei за счёт снижения заселённости более низколежащих
состояний. Колебательные уровни двухатомных молекул в стандартных условиях не
вырождены, чего нельзя сказать о вращательных состояниях. Для них степень
вырождения равна 2J+1, поэтому
распределение Больцмана имеет вид: 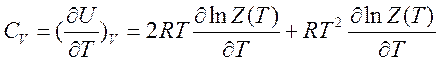 . Максимум заселённости
для CO при 298К соответствует состоянию с
J=7. С ростом температуры максимум
заселённости смещается в сторону больших значений J.
. Максимум заселённости
для CO при 298К соответствует состоянию с
J=7. С ростом температуры максимум
заселённости смещается в сторону больших значений J.
Правила отбора
Квантовые переходы
возможны не для любых пар состояний – существуют определённые сочетания
уровней. Эти переходы определяются правилами отбора. Правила отбора, во-первых,
учитывают симметрию волновых функций исходного и конечного состояний. Кроме
того, должен быть отличен от нуля хотя бы один из интегралов 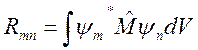 (3). ψm – волновая функция конечного состояния, ψn – волновая функция исходного состояния, M – оператор проекции вектора момента на координатную
ось (соответственно Mx, My или Mz). Правила отбора для
колебательно-вращательных спектров разрешают переходы только между состояниями ∆J=±1 (4). Отметим,
что данное условие определяет ограничение только на вращательное квантовое
число и не зависит от колебательного квантового числа.
(3). ψm – волновая функция конечного состояния, ψn – волновая функция исходного состояния, M – оператор проекции вектора момента на координатную
ось (соответственно Mx, My или Mz). Правила отбора для
колебательно-вращательных спектров разрешают переходы только между состояниями ∆J=±1 (4). Отметим,
что данное условие определяет ограничение только на вращательное квантовое
число и не зависит от колебательного квантового числа.
На самом деле, вероятность перехода уменьшается при увеличении ∆ν. Для условий данной работы (Т=297К) эта зависимость не является существенной в силу очень малой вероятности нахождения частицы в колебательном состоянии, отличном от основного.
Колебательно-вращательные спектры
Последовательность спектральных линий, образующихся при квантовых переходах молекулы, расположенная по длинам волн или частотам даёт картину, индивидуальную для каждого соединения.
Отдельных
колебательных спектров в природе не существует, так как молекулы распределены
по большому количеству вращательных состояний, Энергетический барьер для
перехода с одного вращательного уровня на другой значительно меньше, чем такой
барьер для колебательных состояний, поэтому в действительности наблюдается
смешанный колебательно-вращательный спектр. В нём сигналу, соответствующему
колебательному переходу, сопутствует набор сигналов, отвечающих вращательным
переходам. Колебательно-вращательный терм можно представить так: 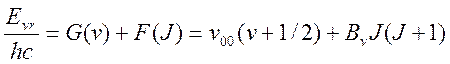 .
.
В соответствие с правилами отбора (4) в спектре наблюдаются две серии линий – соответствующих переходу ∆J=+1 (R-ветвь) и ∆J= –1 (P-ветвь). Ветвь R располагается со стороны больших частот от частоты колебательного перехода, а ветвь P – со стороны меньших частот.
Переход с ∆J=0 запрещён правилами отбора для большинства двухатомных молекул. Объяснение такого ограничения приводят из структуры термов этих молекул. Для монооксида углерода спин-орбитальное взаимодействие ∑-термов равно нулю, поэтому переход с ∆J=0 является запрещённым.
Для молекул с ∑-термом вращательные функции представляют собой сферические гармоники YJ,M(θ,φ). Так как набор сферических гармоник является полным и ортонормированным, то произведение двух сферических гармоник, возникающих в интегралах типа (3) может быть представлена через линейную комбинацию сферических гармоник. Тогда правила отбора для вращательных переходов и дают ограничения ∆J=±1. Для молекул, обладающих термами П, ∆ и др. переход с ∆J=0 является разрешённым.
В случае двухатомной молекулы типа шарового волчка или же многоатомной молекулы запрещение снимается и в спектре проявляется ещё одна ветвь. Её обозначают символом Q. Отсчёт P-линий начинается с J=1, а отсчёт R-линий – с J=0.
Значение J, отвечающее максимуму
интенсивности может быть рассчитано по формуле 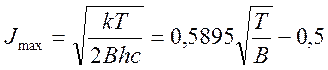 (5).
(5).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.