Определение термодинамических и геометрических характеристик двухатомных молекул из колебательно-вращательных спектров, страница 2

Из колебательно-вращательных спектров можно определить значение вращательной постоянной B. Эта величина связана с моментом инерции молекулы следующим образом: 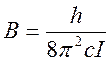, в котором  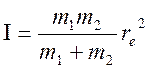– момент инерции. Значение B входит в выражение для вращательной статистической суммы. Проблема заключается в том, что величина B индивидуальна для каждого J. Разные значения J обусловлены отличием моментов инерции, значит,  величина B будет изменяться в  зависимости от J.  Например, для представления линии R-ветви имеем выражение:

 (6.1)

Аналогичное уравнение для P-ветви:

 (6.2)

Для простоты используют приближение, что разность B’–B” мала. Тогда для малых значений J можно считать B’≈ B”≈ B. В действительности, разность B’–B” всегда отрицательна для колебательно-вращательных спектров, поэтому в спектре наблюдается расхождение линий вращательной структуры для P ветви и сближение для R-ветви.

Для приблизительного определения B используют комбинационные разности ∆₂F. Они связаны с вращательной постоянной B и J формулой ∆₂F^X(J)=4B_v^X(J+0,5) (7). Значения комбинационных разностей легко получают из спектра: ∆₂F’=R(J) – P(J) (8.1) или ∆₂F”=R(J – 1) – P(J+1) (8.2).

Обычно для ряда значений J вычисляют комбинационные разности по формулам (8.1) или (8.2) и графически или методом наименьших квадратов определяют соответствующую константу B.

Для лёгких молекул нужно вводить константу центробежного растяжения, что приводит к модификации уравнения (7). (7*).

В данной работе проводили определение величины B методом наименьших квадратов в координатах ∆₂F/(J+1/2) – (J+1/2)². Значение свободного члена равно 4B, а коэффициент пропорциональности равен величине (–8D_V).

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ.

В нашей работе был снят ИК-спектр CO в диапазоне 2260 –2000см^-1, так как из анализа обзорного спектра 3000 – 1000см^-1 видно, что квантовый переход наблюдается в этой области. Из калибровочных отметок 2260 и 2000 см^-1, и масштаба 1мм = 1см^-1, определили положение колебательного перехода 1 – 0. Частота, соответствующая этому колебательному переходу равна 2145см^-1, или 6,435*10¹³ Гц. Видно, что интенсивность линий максимальна для J=6-7, что согласуется с рассчитанным значением J из формулы (4).

Рассчитали комбинационные разности ∆₂F’=R(J) – P(J) и ∆₂F”=R(J – 1) – P(J+1) для значений J=1,2...,7. Полученные значения использовали для отыскания B. Результаты занесли в таблицы (см таблица 1, таблица 2). Таблица 1 построена для ∆₂F’, таблица 2 – для ∆₂F”.

В таблицах приведено приближённое значение B, полученное по формуле (7).