Определение расщепления первой линии Лаймана для атома водорода. Определение вероятности реализации максимального полного спина для спинового состояния, страница 2

Ответ. Электронные конфигурации g⁸ и g¹⁰. Для первой нижним по энергии будет мультиплет ⁹G₀ с энергией –20|l| , для второй – ⁹G₈  с энергией –16|l|.

2. (300) Система из 4 электронов имеет полный спин 2. Определить спиновые функции системы в этом состоянии.

Ответ. Y₁ = aaaa,  Y₂  = ½(aaab + aaba + abaa + baaa), Y₃  = 1/Ö6(aabb + abab + baab + abba + bababbaa),Y₄  = ½(abbb + babb + bbab + bbba), Y₅ = bbbb.

3. (400) Для электронной конфигурации l⁴ определить количество термов с максимальным спином. Какой из них является основным.

Ответ. С максимальным спином 2 количество термов равно 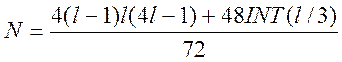, где INT(l/3) = k, при l = 3k, 3k+1 и 3k+3, Эта формула дает: N(d⁴) = 1; N(f⁴) = 5; N(g⁴) = 12. Основной терм .

4. (500) Для электронной конфигурации lⁿ определить энергию и вид нижних по энергии термов в случае jj связи. Конфигурация заполнена менее чем наполовину и n является четным числом.

Ответ. Термы 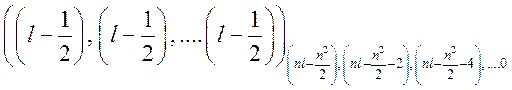имеют наименьшую энергию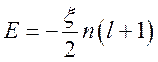

5. (500) Представить расщепление спектральной линии перехода ²P®²S (испускание) в атоме Na в сильном магнитном поле (эффект Пашена-Бака) с учетом слабого спин-орбитального взаимодействия. Объяснить распределение относительных интенсивностей компонент спектра при поперечном наблюдении (магнитное поле вдоль оси Z, регистрация люминесценции перпендикулярно этой оси, например, вдоль оси X).

ML = –1   MS = –½ ∆ELS = +λ/2

Решение. Распределение интенсивностей при эффекте Пашена-Бака при поперечном наблюдении равно 1:2:1 и обусловлено тем, что при заданной геометрии наблюдения вклад в излучение одной из перпендикулярных составляющих осциллятора равен 0 и интенсивность Y компонент будет в 2 раза меньше интенсивности Z. При учете спин-орбитального взаимодействия исчезают все средние по состоянию, кроме L_zS_z  компонент. Смещения даны на рисунке. Крайние линии триплета расщепляются на две с одинаковыми интенсивностями, что приводит к указанному на рисунке распределению.

ML = +1   MS = +½ ∆ELS = +λ/2

 

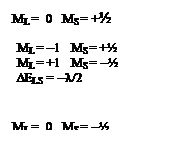Задачи на контрольной 14 ноября 2004 г. (группы 241, 242, 243)

1. (300) Определить все термы конфигурации d⁷, найти спин-орбитальное расщепление основного терма (мультиплеты и их энергии).

Ответ. Для этой конфигурации (вырождение 120) реализуются термы ²H, ²G, ⁴F, ²F, ²D, ²D, ⁴P, ²P (всего 8 термов). Основной терм ⁴F расщепляется на мультиплеты ⁴F_9/2 (-9l/2), ⁴F_7/2 (0), ⁴F_5/2 (7l/2), ⁴F_3/2 (6l). В скобках указаны энергии мультиплетов.

2. (500) Система состоит из трех частиц со спинами S₁ = S, S₂ = S - 1 S₃ = S - 2. Сколько значений полного спина S_полн может реализовать для этой системы? Найти ответ для случаев, когда S – целое и полуцелое числа.

Ответ. При целом S число возможных значений полного спина , при полуцелом -

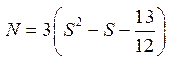
3. (400) Система состоит из трех частиц со спинами S₁ = 2, S₂ = 1 S₃ = 0. Определить функции состояния с минимальным полным спином.

Решение. Минимальный полный спин для этой системы S_полн = 1. Так как для третей частицы с нулевым спином существует всего одна функция |0,0>, найдем вначале функции для системы S₁ = 2, S₂ = 1 с полным спином 1. Первую функцию с проекцией 1 (Y₁ = |1,1>) ищем в виде линейной комбинации

Y₁ = c₁|2,1>|1,0> + c₂|2,0>|1,1> + c₃|2,2>|1,-1>

Использование уравнения S²Y = 2Y позволяет определить коэффициенты в этой линейной комбинации и получить функцию

.

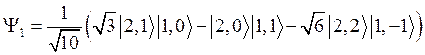Действием оператора понижения L_- = L_1- + L_2- можно найти следующие две функции

.

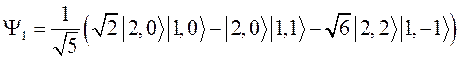
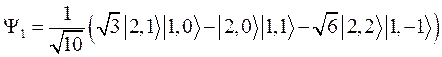Остается умножить эти три функции на функцию |0,0> третьей частицы, и мы получим полный ответ.

4. (400) Определить число линий и расстояние между ними при расщеплении в слабом магнитном поле меньшей по энергии спектральной компоненты (компоненты появляются в результате спин-орбитального взаимодействия) второй линии Бальмера атома водорода (2p¹ ® 3d¹) при поляризации, совпадающей с направлением магнитного поля.

Ответ. Компонента (переход между мультиплетами ²P_3/2 ® ²D_3/2) имеет энергию hn₀ - (l_p/2 + 3l_d/2) и в этой поляризации расщепится на четыре линии, расстояние между которыми равно (8/15)bН.

5. (400) Найти хотя бы один мультиплет, для которого g-фактор равен –10 (минус десять).

Ответ. Можно показать, что в случае J = L – S (L > S) связь между величинами S и L определяется выражением

.

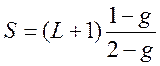Подставляя g = -10, получим 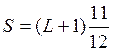. Учитывая, что орбитальный момент L должен быть целым числом, а S – целым или полуцелым, можно найти величины L = 23, S = 22. Таким образом, первый мультиплет имеет вид ⁴⁵23₁.