






Исключая отсюда x, найдем проекцию этой линии на плоскость Oyz: ![]()
![]() . Для потока получим (напомним Замечание 1:
следует учесть, что в этом случае
. Для потока получим (напомним Замечание 1:
следует учесть, что в этом случае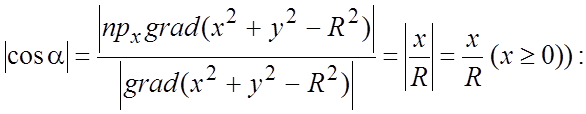
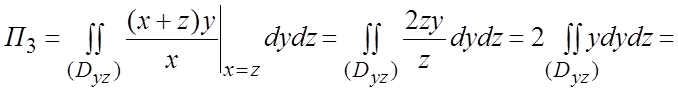
![]()
![]() =
=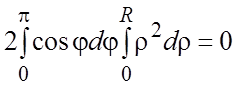 .
4) Для потока
.
4) Для потока ![]() получим
получим 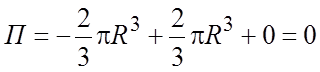 .
.
2°. Метод проектирования на все три
координатные плоскости. Пусть поверхность (S)
однозначно проектируется на все три координатные плоскости: (Dxy): z=z(x,y);
![]() ;
; ![]() .Для
потока П в этом случае имеем (вторая формула из (1.3)):
.Для
потока П в этом случае имеем (вторая формула из (1.3)):
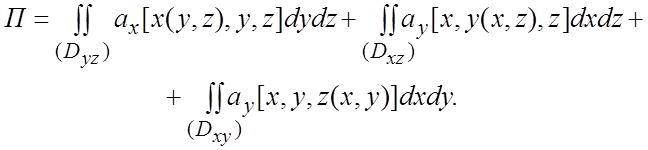 (1.5)
(1.5)
В (1.5) знаки проекций dydz, dxdz, dxdy выбираются в соответствии с сформулированным выше правилом.
Пример 3. Найти поток вектора ![]() через
часть внешней стороны сферы
через
часть внешней стороны сферы ![]() , заключенной в первом
октанте.
, заключенной в первом
октанте.
Решение. Имеем ![]() . С учетом того, что поверхность
расположена в первом октанте, проекции dydz, dxdz, dxdy берем со знаком
“+”. По формуле (1.5)
. С учетом того, что поверхность
расположена в первом октанте, проекции dydz, dxdz, dxdy берем со знаком
“+”. По формуле (1.5) 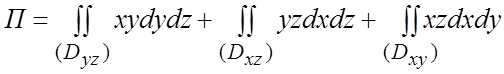 . Из уравнения сферы
имеем:
. Из уравнения сферы
имеем: 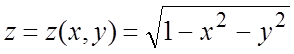 ;
; 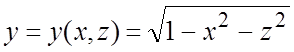 ;
; 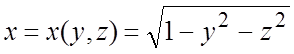 и
и 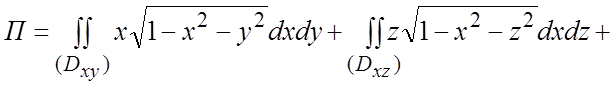
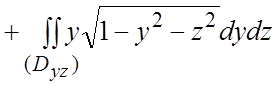 . Очевидно,
. Очевидно, 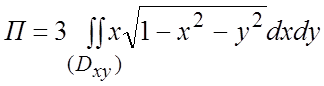 .
Вычислим этот интеграл в полярной системе координат:
.
Вычислим этот интеграл в полярной системе координат: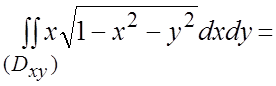
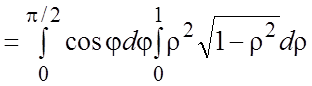 =
=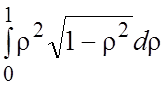 =
=![]() =
=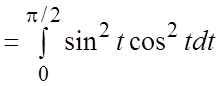
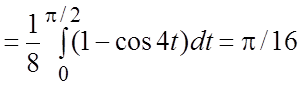 .
Следовательно,
.
Следовательно, ![]() .
.
3°. Применение формулы Гаусса-Остроградского. Приведем соответствующую теорему.
Теорема. Если в некоторой области ![]() проекции
поля
проекции
поля ![]() непрерывны и имеют непрерывные частные
производные
непрерывны и имеют непрерывные частные
производные 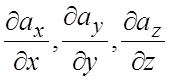 , то поток вектора
, то поток вектора ![]() через произвольную замкнутую кусочно
гладкую поверхность (S), расположенную целиком в
области
через произвольную замкнутую кусочно
гладкую поверхность (S), расположенную целиком в
области ![]() , равен тройному интегралу от суммы
, равен тройному интегралу от суммы 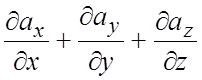 по области (V),
ограниченной поверхностью (S):
по области (V),
ограниченной поверхностью (S):
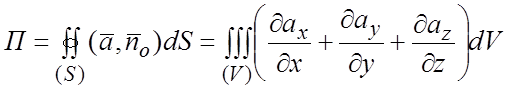 (1.6)
(1.6)
- формула Гаусса-Остроградского.
Замечание.
Подынтегральная функция в тройном интеграле (1.6) называется дивергенцией
(расходимостью) поля ![]() ; обозначается
; обозначается 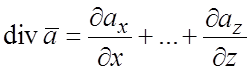 .
.
Пример 4. Вычислить поток вектора ![]() через
замкнутую поверхность
через
замкнутую поверхность ![]() ,
, ![]() .
.
Решение.По формуле (1.6) 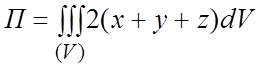 . Для
вычисления этого интеграла применим сферическую систему координат:
. Для
вычисления этого интеграла применим сферическую систему координат: ![]() ,
, ![]() ,
, ![]() ;
; ![]() . Таким
образом,
. Таким
образом, 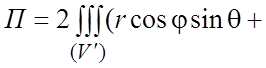
![]()
![]()
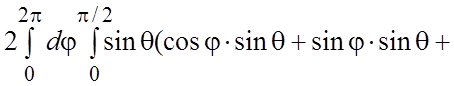
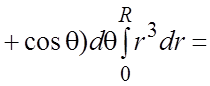
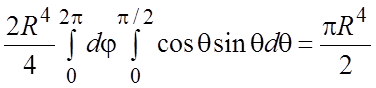 .
.
Пример 5. Используя формулу Гаусса-Остроградского (1.6), вычислить
поток поля 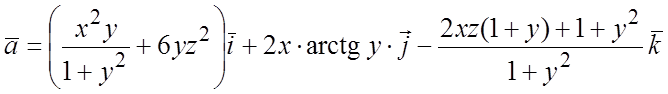 через верхнюю сторону части поверхности
через верхнюю сторону части поверхности ![]() , расположенную над плоскостью Oxy.
, расположенную над плоскостью Oxy.
Решение. Для того, чтобы можно было применить формулу (1.6),
замкнем снизу данную поверхность куском плоскости Oxy,
который ограничен окружностью ![]() , z = 0 . Вычислим подынтегральную функцию, стоящую под
знаком тройного интеграла:
, z = 0 . Вычислим подынтегральную функцию, стоящую под
знаком тройного интеграла: 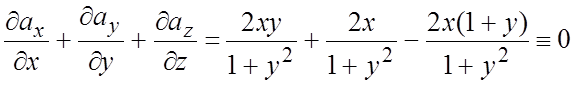 . Отсюда следует, что
поток П=0. По свойству аддитивности
. Отсюда следует, что
поток П=0. По свойству аддитивности ![]() ,
откуда искомый поток
,
откуда искомый поток 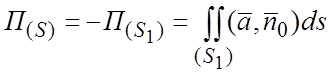 . Уравнение поверхности
. Уравнение поверхности ![]() и
и ![]() . Таким
образом,
. Таким
образом, 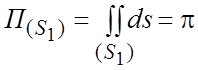 - поток
- поток ![]() через
поверхность z =0 численно равен площади круга
через
поверхность z =0 численно равен площади круга ![]() ; искомый поток
; искомый поток ![]() .
.
15.1.3. Линейный интеграл вектора. Циркуляция векторного поля
Пусть
поле ![]() - непрерывное векторное поле, (L) – кусочно гладкая кривая с выбранным на ней
положительным направлением (ориентированная кривая).
- непрерывное векторное поле, (L) – кусочно гладкая кривая с выбранным на ней
положительным направлением (ориентированная кривая).
Определение 1. Линейным интегралом (обозначается L) вектора ![]() вдоль
ориентированной кривой (L) называется
криволинейный интеграл
вдоль
ориентированной кривой (L) называется
криволинейный интеграл
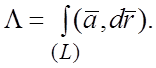 (1.7)
(1.7)
Для линейного интеграла справедливы следующие формулы:
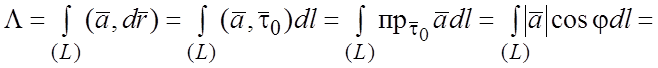 (1.8)
(1.8)
=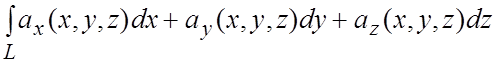 .
.
Если поле ![]() есть силовое поле
есть силовое поле ![]() ,
то линейный интеграл (1.7) дает величину работы этого поля вдоль линии (L). Вычисление линейного интеграла в зависимости от
задачи может быть проведено по одной из формул “списка” (1.8).
,
то линейный интеграл (1.7) дает величину работы этого поля вдоль линии (L). Вычисление линейного интеграла в зависимости от
задачи может быть проведено по одной из формул “списка” (1.8).
Определение 2. Циркуляцией (обозначается Ц) векторного поля
![]() называется линейный интеграл по замкнутой
ориентированной кривой (L):
называется линейный интеграл по замкнутой
ориентированной кривой (L):
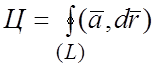 .
(1.9)
.
(1.9)
За положительное направление обхода замкнутой кривой (L) берется то, при котором область, ограниченная кривой, лежит под левой рукой.
Пример 1. Найти линейный интеграл вектора ![]() вдоль
дуги (L) винтовой линии
вдоль
дуги (L) винтовой линии ![]() от
точки A пересечения линии с плоскостью z=0 до точки В пересечения с плоскостью z =1.
от
точки A пересечения линии с плоскостью z=0 до точки В пересечения с плоскостью z =1.
Решение. Имеем по последней формуле из списка (1.8): 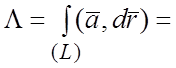
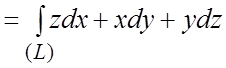 . Точке A соответствует значение параметра t
=0, точке B – значение
. Точке A соответствует значение параметра t
=0, точке B – значение ![]() и,
таким образом,
и,
таким образом, 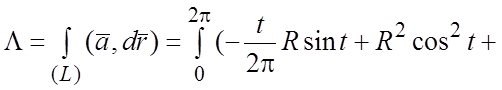
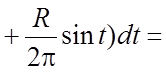
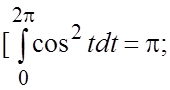
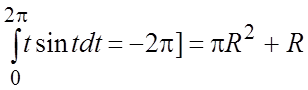 .
.
Пример 2. Вычислить работу силового поля ![]() вдоль
отрезка
вдоль
отрезка ![]() прямой, проходящей через точки
прямой, проходящей через точки ![]() и
и ![]() .
.
Решение. Работа 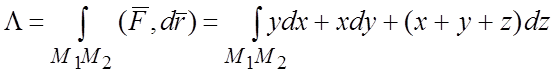 .
.
Запишем
канонические уравнения прямой 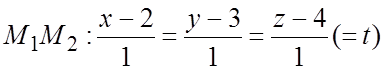 .
.
Отсюда ![]() ; параметры
; параметры ![]() .
Вычислим работу:
.
Вычислим работу:
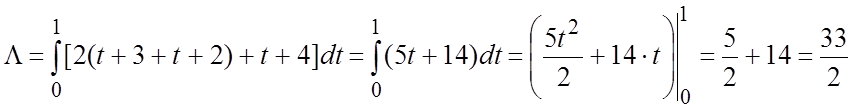 .
.
Пример 3. Вычислить циркуляцию поля ![]() вдоль
эллипса
вдоль
эллипса 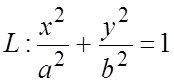 .
.
Решение. Имеем по формуле (1.9) и (1.8): 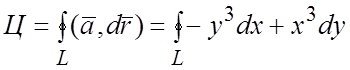 .
.
Запишем параметрические уравнения эллипса: ![]() . Вычисляя
dx и dy, получим:
. Вычисляя
dx и dy, получим:
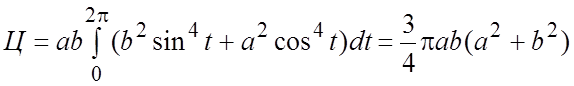 - здесь использовано, что
- здесь использовано, что 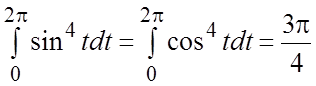 (вычисление этих интегралов проводится с
помощью понижения степени подынтегральной функции).
(вычисление этих интегралов проводится с
помощью понижения степени подынтегральной функции).
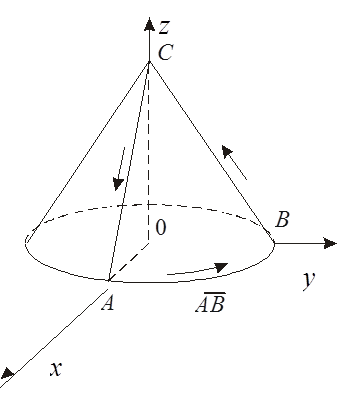 Пример 4. Вычислить циркуляцию векторного поля
Пример 4. Вычислить циркуляцию векторного поля ![]()
![]() вдоль линии L, полученной пересечением конуса
вдоль линии L, полученной пересечением конуса ![]() с
координатными плоскостями (см. рис.4).
с
координатными плоскостями (см. рис.4).
|
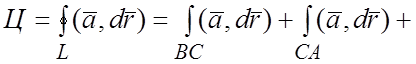
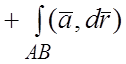 .1)
На отрезке BC имеем:
.1)
На отрезке BC имеем: 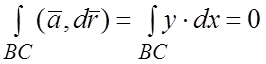 . 2) На отрезке CA имеем:
. 2) На отрезке CA имеем: 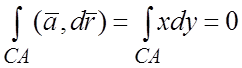 . 3) На дуге AB
окружности
. 3) На дуге AB
окружности 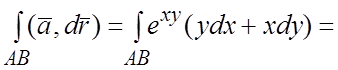
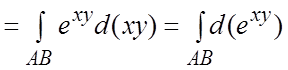 =
=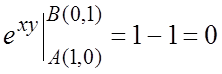 . Искомая циркуляция
поля равна нулю.
. Искомая циркуляция
поля равна нулю.
Пример 5. Вычислить циркуляцию векторного поля ![]() вдоль линии
вдоль линии ![]() ,
, ![]() .
.
Решение. Имеем: 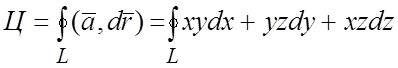 . Линия L есть эллипс, получающийся в результате сечения цилиндра
. Линия L есть эллипс, получающийся в результате сечения цилиндра
![]() плоскостью
плоскостью ![]() .
Найдем параметрические уравнения этой линии. Проекция любой точки этой линии на
плоскость Oxy находится на окружности
.
Найдем параметрические уравнения этой линии. Проекция любой точки этой линии на
плоскость Oxy находится на окружности ![]() . Отсюда, полагая
. Отсюда, полагая ![]() ,
найдем, что
,
найдем, что ![]() . Для z из
уравнения
. Для z из
уравнения ![]() получим:
получим: ![]() . Таким
образом,
. Таким
образом, ![]()
![]()
![]() . Находим отсюда:
. Находим отсюда: ![]()
![]()
![]() , и для циркуляции
запишем определенный интеграл:
, и для циркуляции
запишем определенный интеграл: 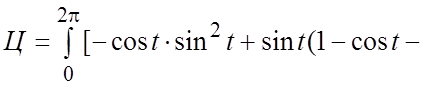
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.