Составление дифференциальных уравнений плоскопараллельного движения

Страницы работы

1 страница (Word-файл)

Содержание работы

Задание для контрольной работы по теоретической механике (динамика Д4)

Барабан радиуса R весом Р имеет заточку (как у катушки) радиуса r=0.6R. К концам намотанных на барабан нитей приложены постоянные силы F₁ и F₂, направления которых определяются углом b. Кроме сил на барабан действует пара с моментом М, направление которого показано на рисунке. При движении, начинающемся из состояния покоя, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона a. Пренебрегая сопротивлением качению, определить закон движения центра масс барабана х_С=f(t), и наименьшее значение коэффициента трения k о плоскость, при котором возможно качение без скольжения. Барабан считать сплошным однородным цилиндром радиуса R. Данные для расчета: a=30^о, b=60^о, F₁=0, F₂=0.4P, M=0.

Решение задачи

Барабан совершает плоскопараллельное движение под действием сил P, F₁, F_2,, N, F_тр и момента М. Так как направление силы трения F_тр заранее неизвестно, выбираем его произвольно. Проведем оси Oxy и составим дифференциальные уравнения плоскопараллельного движения.

(1)

(2)

(3)

За положительное направление моментов в уравнении (3) принято направление против хода часовой стрелки, то есть в ту сторону, куда будет вращаться барабан при движении центра С от оси Oy (это равноценно предположению, что барабан будет катиться вверх по наклонной плоскости, то есть вращаться против хода часовой стрелки).

1. Определение x_C=f(t). Так как ясно, что в нашем случае y_C=R=const и , то уравнения (1)-(3) содержат четыре неизвестных величины (). Используем дополнительно условие отсутствия проскальзывания барабана по наклонной плоскости в виде v_C=wR или, что то же самое, . Теперь из уравнения (3) можно исключить угловое ускорение e, подставив в него найденной значение и деля его на R. В результате получим:

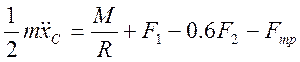(4)

Сложив теперь уравнения (1) и (4), а также учитывая, что М=0 и F₁=0 ,а F₂=0.4P=0.4mg, P=mg , можно получить:

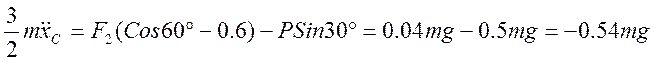или ;

Дважды интегрируя последнее выражение получим x_C= - 0.18gt²+ C₁t + C₂. Из начальных условий (x_C=0,v_C=0 при t=0) получаем, что С₁=С₂=0. Окончательно получаем искомую зависимость в виде

x_C= - 0.18gt² (вопреки нашему первоначальному предположению барабан катится вниз по наклонной плоскости).

2. Определение k_min. Для нахождения наименьшего значения k получим из уравнения (2) значение N:

N= - F₂Sin60°- F₁ Sin60°+Pcos30°=0.52P;

Силу трения F_тр найдем из уравнения (4) подставив в него найденное значение и учитывая, что М=0, F₁=0, F₂=0.4P, mg=P :

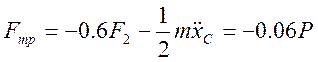
Знак указывает, что сила F_тр направлена на самом деле вниз (противоположно показанному на рисунке).

Для определения минимально необходимого значения коэффициента трения k исходим из того, что при качении без проскальзывания сила трения должна удовлетворять неравенству . Подставляя сюда найденные значения F_тр и N получим . Следовательно, наименьший коэффициент трения, при котором возможно качение барабана без проскальзывания (при заданном значении силы F₂) k_min=0.12.