Кинетика физико-химических процессов в реагирующих газовых средах, страница 4

Точка, описывающая состояние активированного комплекса, движется вдоль пути реакции со скоростью порядка скоростей относительного движения атомов, т. е. со средней скоростью  порядка тепловой. Время пребывания ее на отрезке , т. е. время жизни активированного комплекса порядка . Для характерных см и см/c cи время жизни комплекса много меньше характерного времени реакции (времени достижения химического равновесия в смеси газов), что дает обоснование высказанному выше утверждению (9.21).

Если считать, что каждый образовавшийся комплекс распадается в сторону продуктов реакции, то число актов реакции в ед. объема и в ед. времени равно числу распадов комплекса, т. е. числу комплексов в ед. объема, поделенному на время их жизни. Обозначив через  плотности реагентов, а  комплексов (для реакции (9.21)  есть  и , а ), получим для прямой реакции

                                                                                  (9.22), откуда константа скорости прямой реакции есть

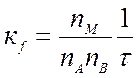                                                                                           (9.23).

По закону действующих масс отношение чисел частиц, участвующих в реакции , в состоянии равновесия равно отношению статистических сумм частиц. Как и ранее, разделим обе части равенства на объем, занимаемый газом (с учетом того, что объем  входит линейным множителем только в поступательные статистические суммы), выделим из статистических сумм множители типа , соответствующие энергии частиц в основном состоянии, и замечая, что  равно энергии активации, получим

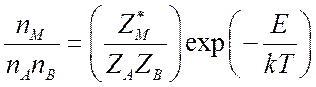                                                                  (9.24).

В статистической сумме переходного комплекса необходимо учесть то, что поступательное движение комплекса вдоль координаты реакции считается независящим от других степеней свободы. Поэтому полная статистическая сумма  должна быть представлена в виде двух сомножителей: трансляционной (поступательной) статсуммы на участке  вдоль координаты реакции  равной 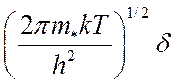, где  эффективная масса комплекса и статсуммы для остальных степеней свободы комплекса :

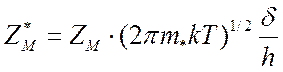                                                                                 (9.25).

Подставляя (9.24) и (9.25) в (9.23) с учетом , где  - средняя скорость поступательного движения вдоль координаты разложения, для константы скорости получим

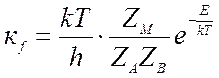                                                                                          (9.26).

Следует отметить, что неопределенные величины  и  сократились и в конечное выражение для константы реакции не входят. Вводят еще так называемый трансмиссионный коэффициент , характеризующий вероятность распада комплекса  в сторону продуктов реакции, который обычно порядка единицы и окончательно

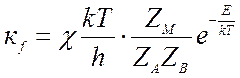                                                                                       (9.27).

          Вычисление статсумм в уравнении (9.27) производится с использованием представления  в виде произведения поступательной, вращательной, колебательной и электронной статсумм

                                                                                (9.28).

 равно кратности электронного вырождения молекулы, а  вычисляются на основе стандартных формул статистической физики:

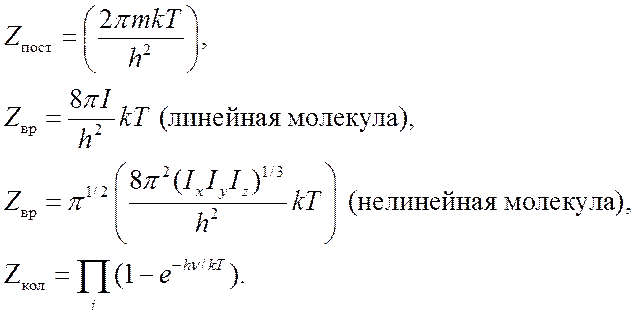                               (9.29).

Для поступательной статсуммы комплекса , а объем, входящий в качестве сомножителя в формулу опущен.

          Самым слабым местом в теории МПС является вопрос конструирования переходного комплекса, что часто дает повод к утверждению, что по МПС можно получить любое значение константы скорости, стоит только соответствующим образом сконструировать переходной комплекс.