Изучение структуры молекулярного спектра двухатомной молекулы

Работа 1.3. «Изучение структуры молекулярного спектра двухатомной молекулы»

Цель работы: исследование структуры спектра поглощения молекулы йода, установление закономерностей электронно-колебательно-вращательных переходов в двухатомной молекуле, определение спектроскопическим методом энергии диссоциации, величины колебательного кванта и постоянной ангармоничности колебаний для молекулы I2 в основном и электронно-возбужденном состояниях.

Краткая теория

Молекулярные спектры поглощения и излучения содержат колебательную и вращательную структуру молекул веществ.

Химическое и пространственное строение молекул объясняется квантовой механикой с помощью приближения Борна-Оппенгеймера:

, где r, R– электронные и ядерные координаты.

Полная энергия молекулы при этом равна сумме энергии электронов и энергии ядра.

Электронные термы находятся по измеренным уровням энергии E_n(R), где R – межъядерное расстояние. Если E_n(R) имеет минимум, то такое состояние связное, иначе распадное. Однако, существуют молекулы у которых в основном состоянии нет минимума, а в возбужденном он появляется, что говорит о возможности существования  таких молекул только в возбужденном состоянии.

Колебательно-вращательная структура

При заданном электронном состоянии движение ядер есть движение точечных частиц, взаимодействующих между собой с потенциалом E_n(R). Положение двух ядер задается шестью координатами, определяющими движение молекулы как целого, вращение молекулы и радиальное движение ядер (колебания). При этом уравнение Шредингера в системе центра масс имеет следующее факторизованное по угловым и радиальным переменным решение:  . Радиальное движение происходит в потенциале 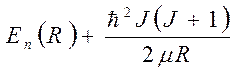, где µ – приведенная масса ядра + оболочки электронов.

При малых J вклад центробежного потенциала мал и R можно заменить на R_e(равновесное межъядерное расстояние), при этом , где 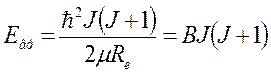, B – вращательная постоянная.

Колебательная структура хорошо описывается потенциалом Морзе:, где a – постоянная, а x= R –R_e, где D – глубина потенциальной ямы, определяющая энергию диссоциации молекул (за вычетом нулевых колебаний). Разлагая потенциал Морзе вблизи R_e , получим равновесную частоту ангармонических колебаний системы: .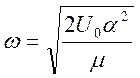

Уравнение Шредингера с потенциалом Морзе допускает точного решения и энергетический спектр частицы представляется в виде: 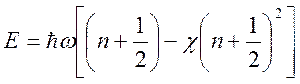. Из условия экстремальности спектра Морзе получим связь: . .

Правила отбора

Молекулы характеризуются набором квантовых чисел (N, J, n), где N – совокупность квантовых чисел, характеризующих состояние электронов.

Вращательный переход – (N, J", n) ↔ (N, J', n): , d(R_e) ≠ 0.

Колебательно-вращательный переход – (N, J", n") ↔ (N, J', n'): ,(гармонический потенциал), (ангармонический потенциал), .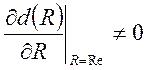

В гомоядерных молекулах в пределах одного электронного терма запрещены как вращательные, так и колебательно-вращательные переходы.

Электронно-колебательно-вращательные переходы – ΔS = ΔSz = 0, должен сохраняться знак Σ-состояния, для гомоядерных молекул разрешены только переходы между состояниями разной четности g ↔ u. Помимо условия ΔJ = ±1 возникает возможность перехода без изменения вращательного квантового числа ΔJ = 0, но только не между Σ-состояниями и не между состояниями с J = 0.

Принцип Франка-Кондона: электронный переход в молекуле совершается настолько быстро по сравнению с колебательным движением, что при этом ни межъядерное расстояние, ни скорости движения ядер практически не меняются.

Поэтому вероятность перехода будет максимальной, если ядерные волновые функции начального и конечного состояний локализованы в одной и той же области пространства. В итоге матричный элемент перехода оказывается пропорционален интегралу перекрытия ядерных волновых функций, описывающих начальное и конечное состояние ядерной подсистемы и принадлежащих различным электронным термам молекулы: .

Квадрат интеграла перекрытия называется фактором Франка–Кондона F. Он определяет относительную вероятность заселения конкретного уровня n' при переходах (N”, J", n") → (N’, J', n'), или уровня n" при переходах (N', J', n') → (N", J", n").

Электронно-колебательно-вращательный спектр поглощения двухатомной молекулы