Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (задание на курсовую), страница 2

Изображения простых сигналов

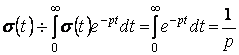;                                                              (2)

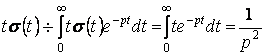.                                                         (3)

Применяя свойства линейности и временного сдвига и учитывая (2) и (3), получим изображение сигнала (1)

.

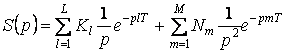3. Для перехода от изображения  к спектральной плотности  сигнала достаточно заменить аргумент  на аргумент . Это правомерно, так как все, приведенные в задании сигналы, являются абсолютно интегрируемыми. Используя формулу Эйлера и основные тригонометрические равенства, выражение для спектральной плотности рекомендуется преобразовать к виду

,                                                                                  (4)

где – момент времени, определяющий центр или линию симметрии сигнала.

Функцию  рекомендуется представлять в виде произведения элементарных функций

.

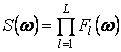Такое представление упрощает нахождение амплитудного и фазового спектров сигнала и их анализ:

,

.

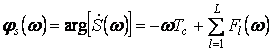Например,

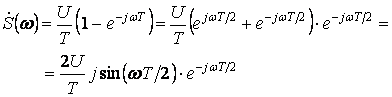.                                (5)

Тогда модуль

.

При нахождении фазы учтем, что  при  и  при , а  – вещественная функция, принимающая положительные и отрицательные значения, что соответствует значениям фазы 0 и , что соответствует скачку фазы на  при каждой смене знака функции. Тогда

,

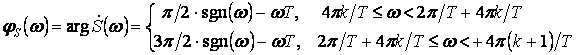где  – сигнум-функция;

.

4. Для нахождения коэффициента передачи цепи рекомендуется преобразовать ее к эквивалентной цепи, показанной на рисунке 3.

 

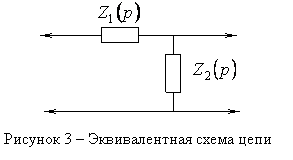Как видно из рисунка, цепь представляет собой делитель напряжения, поэтому передаточная функция цепи

.

Выражение для передаточной функции рекомендуется приводить к виду

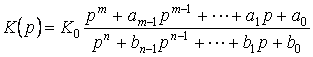.                                               (6)

Цепь является устойчивой, поэтому для перехода к частотному коэффициенту передачи  достаточно заменить  на . Амплитудно-частотная и фазочастотная характеристика цепи находятся аналогично амплитуд ному и фазовому спектрам сигналов.