


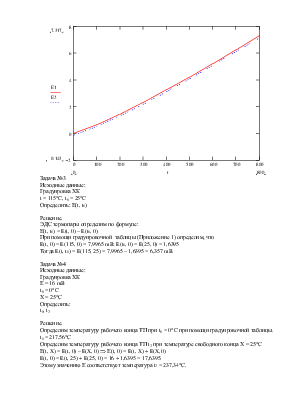


Расчетное задание.
Задание: Рассчитать диаметр отверстия диафрагмы, установленной на участке трубопровода, при котором максимальному перепаду давления Δр соответствовал бы максимальный расход Qм = 80 т/час. Рассчитать также величину безвозвратных потерь напора, соответствующую максимальному расходу
Исходные данные:
Диаметр трубопровода при нормальной температуре (20°С) D20 = 200 мм;
Материал трубопровода Сталь 20;
Материал диафрагмы Сталь 1Х18Н9Т;
Давление перед диафрагмой р1 = 100 кгс/см2;
Температура пара t = 400 °С;
Перепад давления Δр = 0,4 кгс/см2;
Решение.
Диаметр трубопровода при рабочей температуре
![]() ,
,
где ![]() выбирается из таблицы 15.1 (С.
Ф. Чистяков, Д. В. Радун Теплотехнические измерения и приборы) в зависимости от
рабочей температуры и материала трубопровода.
выбирается из таблицы 15.1 (С.
Ф. Чистяков, Д. В. Радун Теплотехнические измерения и приборы) в зависимости от
рабочей температуры и материала трубопровода.
![]()
D = 200 мм∙1,0052 = 201,04 мм
Определим плотность пара при р = 100 кгс/см2 и t = 400°С из таблиц теплофизических свойств воды и водяного пара.
р = 100 кгс/см2 = 9,8066 МПа
r = 36,9467 кг/м3
Определим средний расход.
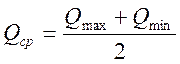
Известно, что для данного способа определения расхода 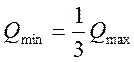
Тогда 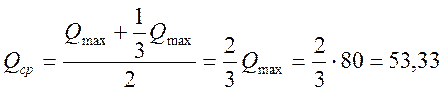 т/ч
т/ч
Определим произведение am из формулы (15-14) (С. Ф. Чистяков, Д. В. Радун Теплотехнические измерения и приборы):
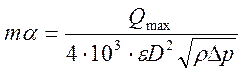 ,
,
где e - поправочный множитель, учитывающий сжимаемость среды. В первом приближении принимаем, что пар не сжимаем, тогда e = 1.
Δр = 0,4 кгс/см2 = 39226,4 Па
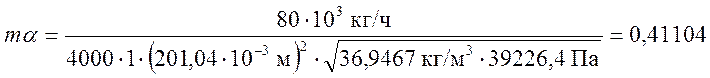
Воспользуемся таблицей 15.3 (С. Ф. Чистяков, Д. В. Радун Теплотехнические измерения и приборы) для составления таблицы коэффициентов a и am для диаметра трубопровода D = 200 мм в зависимости от модуля диафрагмы m.
|
m |
0,05 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,65 |
0,7 |
|
a |
0,604 |
0,607 |
0,618 |
0,637 |
0,663 |
0,699 |
0,7445 |
0,773 |
0,808 |
|
am |
0,0302 |
0,0607 |
0,1236 |
0,1911 |
0,2652 |
0,3495 |
0,4467 |
0,50245 |
0,5656 |
Вычисленное значение am соответствует значениям m, принадлежащим интервалу 0,5¸0,6.
При помощи линейной интерполяции определим точное значение m.
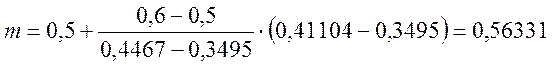
Определим e во втором приближении.
Поправочный множитель e зависит от модуля m, показателя адиабатического расширения, а также от отношения Δрср/р1.
Определим отношение Δрср/р1.
Из формулы (15-29)
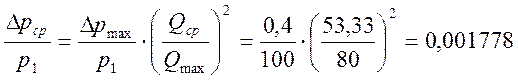
Показатель адиабатического расширения определяем из таблицы 15.5 в зависимости от рабочей температуры пара.
При t = 400°С c = 1,29
Определим e по формуле:
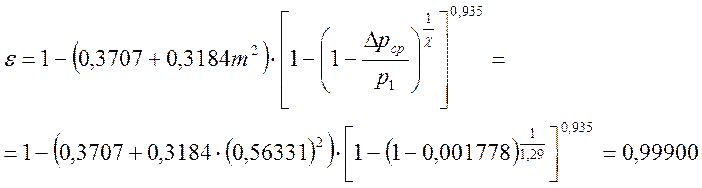
Определяем am во втором приближении, поскольку разница между значениями e, полученными в первом и во втором приближении больше чем 0,0005
e1 - e2 = 1 – 0,99900 = 0,001 > 0,0005
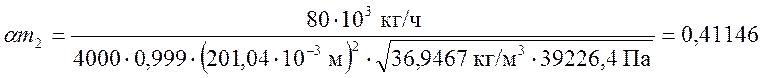
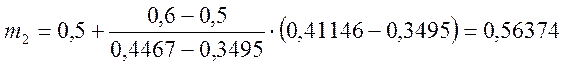
Принимаем окончательно m = 0,56374.
Определяем число Рейнольдса для среднего значения расхода по формуле (15-22):
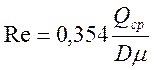 ,
,
где D в [мм];
m - коэффициент динамической вязкости пара, определяется по таблицам теплофизических свойств воды и водяного пара, при соответствующих параметрах.
m = 2,4477∙10-5 Па∙с
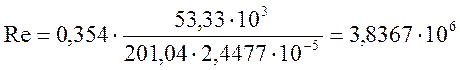
Определяем Reгр из таблицы на странице 214 учебника
Reгр = 220057
Так как Re > Reгр, то вычисленное значение модуля m можно принять.
Определяем диаметр отверстия диафрагмы при рабочей температуре.
![]() мм
мм
Определяем диаметр отверстия диафрагмы при нормальной температуре.
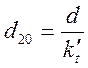 ,
,
где ![]() - коэффициент термического
расширения материала диафрагмы, определяется из таблицы 15.1 в зависимости от
материала диафрагмы и рабочей температуры.
- коэффициент термического
расширения материала диафрагмы, определяется из таблицы 15.1 в зависимости от
материала диафрагмы и рабочей температуры.
![]()
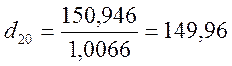 мм
мм
Величину безвозвратных потерь напора определим из таблицы 15.2 в зависимости от модуля m.
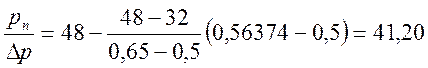 %,
%,
тогда рn = 0,412∙0,4 = 0,165 кгс/см2
Домашние задачи.
Задача №1
Исходные данные:
ТП – Fe-Cu
t1 = 100°C; t2 = 50°C; t0 = 0°C
Определить: E(t1, t0); E(t2, t0)
Решение.
Руководствуясь рекомендациями для определения термо-ЭДС нестандартных термопар, изложенных в §4.2 учебника (С. Ф. Чистяков, Д. В. Радун Теплотехнические измерения и приборы), запишем выражение для термо-ЭДС пары Fe-Cu.
ЕFe-Cu(t, t0) = EPt-Fe(t, t0) + EPt-Cu(t, t0)
Воспользуемся таблицей 4.1 из этого учебника для определения термо-ЭДС пар Pt – Fe, Pt – Cu при t1 = 100°C, t0 = 0°C.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.