Расчет диаметра отверстия диафрагмы, установленной на участке трубопровода, страница 2

E_Pt-Fe(100, 0) = +1,8 mB

E_Pt-Cu(100, 0) = +0,75 mB

Тогда Е_Fe-Cu(100, 0) = +1,80 + 0,75 = 2,55 mB.

Если считать, что термо-ЭДС термопар Pt – Fe и Pt – Cu линейно зависит от температуры рабочего конца при неизменной температуре свободного конца (t₀ = 0°С = const), то для пары Fe – Cu можно записать:

E_Fe-Cu(50, 0) = 0,5∙Е_Fe-Cu(100, 0) = 0,5∙(2,55) = 1,275 mB.

Задача №2

Исходные данные:

Градуировка ПП-1

Х = 25°С

Решение.

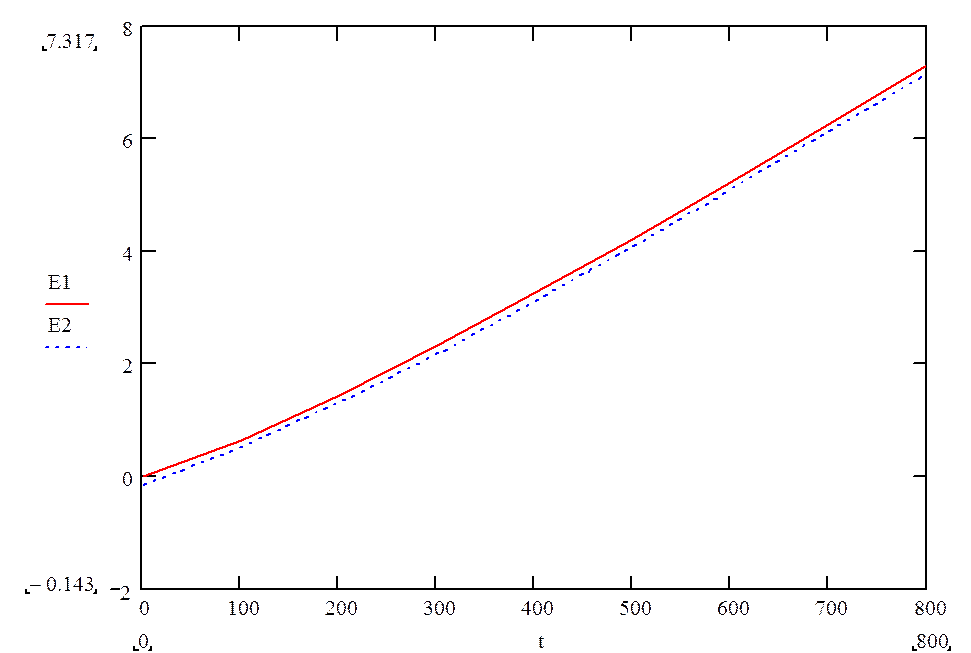
Для построения первой зависимости Е = Е(t, 0) воспользуемся градуировочной таблицей (Приложение 3 Методические указания к лабораторным работам).

t, °C	0	100	200	300	400	500	600	700	800
E, mB	0	0,644	1,436	2,314	3,250	4,216	5,218	6,253	7,317

Для построения зависимости Е = Е(t, Х), где Х = 25 °С воспользуемся формулой.

Е(t, X) = E(t, 0) – E(X, 0)

E(25, 0) = 0,143

Тогда

t, °C	0	100	200	300	400	500	600	700	800
E, mB	-0,143	0,501	1,293	2,171	3,107	4,073	5,075	6,110	7,174

Задача №3

Исходные данные:

Градуировка ХК

t = 115°C, t₀ = 25°C

Определить: Е(t, t₀)

Решение.

ЭДС термопары определим по формуле:

Е(t, t₀) = E(t, 0) – E(t₀, 0)

При помощи градуировочной  таблицы (Приложение 1) определим, что

E(t, 0) = E(115, 0) = 7,9965 mB; E(t₀, 0) = E(25, 0) = 1,6395

Тогда E(t, t₀) = E(115, 25) = 7,9965 – 1,6395 = 6,357 mB.

Задача №4

Исходные данные:

Градуировка ХК

Е = 16 mB

t₀ = 0°C

Х = 25°С

Определить:

t₁, t₂

Решение.

Определим температуру рабочего конца ТП при t₀ = 0°C при помощи градуировочной таблицы.

t₁ = 217,56°С

Определим температуру рабочего конца ТП t₂ при температуре свободного конца Х = 25°С

Е(t, X) = E(t, 0) – E(X, 0) Þ Е(t, 0) = E(t, X) + E(X,0)

E(t, 0) = E(t, 25) + E(25, 0) = 16 + 1,6395 = 17,6395.

Этому значению Е соответствует температура t₂ = 237,34°С.

Задача №5

Исходные данные:

Градуировка ХК

t₀₁ = 0°C; t₀₂ = 25°C

t₁ = 100°C; t₂ = 200°C

Определить k₁, k₂

Решение.

Согласно определению коэффициент преобразования – это отношение развиваемой ЭДС к температуре рабочего конца.

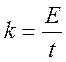
Определим термо-ЭДС ТП при t₀₁ = 0°C и t₁ = 100°C, t₂ = 200 °С

Е(t₁, 0) = E(100, 0) = 6,898 mB;

E(t₂, 0) = Е(200, 0) = 14,570 mB

Тогда

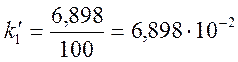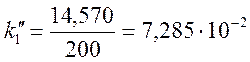 mB/°C;  mB/°C

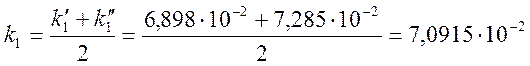
Определим термо-ЭДС при t₀₂ = 25 °C и t₁ = 100°C, t₂ = 200°C

E(t₀₂, 0) = E(25, 0) = 1,6395 mB

Е(100, 25) = Е(100, 0) – Е(25, 0) = 6,898 – 1,6395 = 5,2585 mB;

Е(200, 25) = Е(200, 0) – Е(25, 0) = 14,570 – 1,6395 = 12,9305 mB

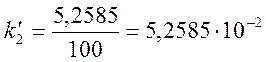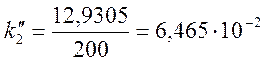 mB/°C;  mB/°C

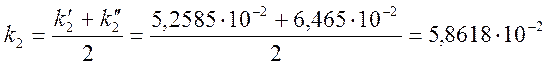
Задача №6

Исходные данные:

Е₁ = 21,13 mB;

t₁ = 300°C;

E₂ = 29,75 mB;

t₂ = 400°C

Определить градуировку

Решение.

Е(t, t₀) = E(t, 0) – E(t₀, 0)

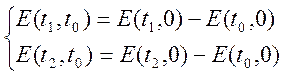
E(t₁, t₀) – E(t₂, t₀) = E(t₁, 0) – E(t₂, 0)

E(t₂, t₀) – E(t₁, t₀) = E₂ – E₁ = 29,75 – 21,13 = 8,62 mB

Рассчитаем чему будет равна разница E(t₂, 0) – E(t₁, 0) для стандартных термопар.

ХК: Е(400, 0) – Е(300, 0) = 31,48 – 22,88 = 8,60.

Данный результат наиболее близко подходит для полученной разницы E₂ – E₁.

Итак, градуировка ТП – ХК

Задача №10

Исходные данные:

R_м = 1000 Ом;

R_л = 15 Ом;

t = 60°С;

t₀ = 20°С;

провода – медные

Определить:

dU

Решение.

Сопротивление проводящих линий при температуре t₀.

R_л = R₀(1 + at₀),

где a = 4,26×10^-3 К^-1 – температурный коэффициент сопротивления медного проводника.

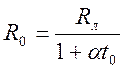
Сопротивление проводящих линий при температуре t.

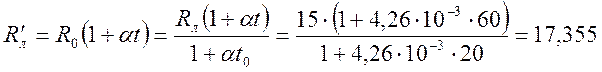Ом

Показания вольтметра при температуре t₀.

U₂₀ = E - I×R_л

Показания вольтметра при температуре t.

U₆₀ = E -

В соответствии с законом Ома для полной цепи можно записать:

;

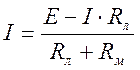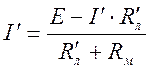
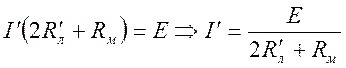
Аналогично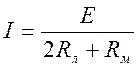

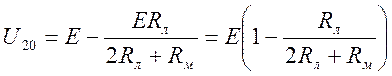
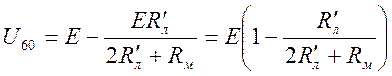
Разность в показаниях вольтметра при температурах t₀ и t.

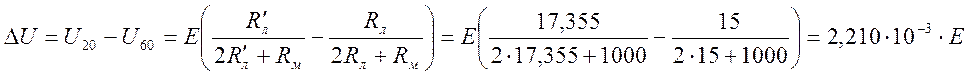
Относительная погрешность вольтметра.

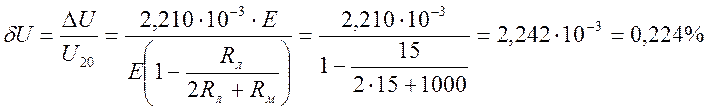
При проведении измерений с помощью потенциометра изменение температуры проводящих линий не скажется на точности показаний прибора.