Анализ спектров и нелинейных искажений, страница 6

Если сигнал содержит только одну гармоническую составляющую и ее частота не совпадет с какой-либо частотой сетки частот ДПФ, то после вычисления ДПФ отрезка сигнала будет получено много не равных нулю составляющих. Максимальную амплитуду будут иметь две составляющие с частотами сетки, «окружающими» частоту составляющей сигнала, однако их амплитуды будут меньше амплитуды составляющей сигнала (эффект распределения энергии одной составляющей сигнала на сетку частот).

Все это ухудшает как точность измерения амплитуд гармонических составляющих исследуемого сигнала, так и разрешающую способность анализа – способность различить две близкие по частоте гармонические составляющие.

Средством борьбы с этим является применение временного окна – вещественной функции, на которую умножается последовательность отсчетов сигнала. Применяют различные временные окна – прямоугольные, Хемминга, Хеннинга, Кайзера и т.д. Общей их особенностью является симметричность относительно середины отрезка сигнала, малое (близкое к нулю) значение в начале и конце отрезка сигнала и максимальное значение в середине сигнала. Применение временного окна чем-то похоже на медленную регулировку «громкости» исследуемого сигнала – сначала она маленькая, затем к середине отрезка сигнала нарастает до максимума, а к концу сигнала спадает до минимума. В целом это приводит к уменьшению «эффективной» длины используемого отрезка сигнала и, как следствие, распределению энергии одной гармонической составляющей на несколько соседних частот частотной сетки ДПФ (независимо от частоты этой составляющей). Т.е. разрешающая способность (по частоте) спектрального анализа ухудшается, но уменьшается погрешность определения амплитуд составляющих сигнала из-за априорной неизвестности их частот.

Важно знать, что повышение разрешающей способности (по частоте) анализаторов спектра определяется используемой длительностью исследуемого сигнала: чем выше должна быть разрешающая способность (т.е. меньше разность частот различаемых спектральных составляющих), тем больше должна быть длительность исследуемого сигнала.

В фильтровых анализаторах это определяется полосой пропускания анализирующего фильтра и связанной с ней длительностью переходного процесса в фильтре (для повышения разрешающей способности необходимо сузить полосу пропускания фильтра, из-за чего повысится длительность переходного процесса в фильтре, а вместе с ней и необходимая длительность исследуемого сигнала).

В цифровых анализаторах спектра для повышения разрешающей способности по частоте необходимо «угущать» расчетную сетку частот, что достигается только увеличением «эффективной» длительности используемого отрезка сигнала.

4. Параметры исследуемых колебаний, определяемые по их спектрам

Аппаратурный спектральный анализ используют обычно для выявления «неправильных» составляющих в спектре исследуемого колебания, характеризующих его "не качественность"; измерение уровня амплитуд таких составляющих по отношению к амплитудам "правильных" составляющих дает количественную оценку качества исследуемого колебания. Ниже даются определения некоторых параметров колебаний, определяемых с помощью анализатора спектра.

В данной лабораторной работе анализаторы спектра будут использоваться для оценки качества выходных колебаний генератора сигналов низкочастотного Г3‑118, генератора сигналов специальной формы SFG-2110 и функционального генератора присоединительного устройства BNC‑2120.

4.1. Коэффициент гармоник – отношение среднеквадратического отклонения суммы высших гармоник исследуемого напряжения к среднеквадратическому отклонению первой гармоники исследуемого напряжения:

.

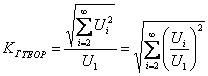С помощью анализатора спектра измеряются парциальные коэффициенты гармоник

 ,