Определение тепловых свойств твердых тел методом регулярного режима: Методические указания к лабораторной работе, страница 4

№ п/п
1	0
2	30
3	60
4	90
5	120
.	.
.	.
.	.
≈40	.

Таблица 2 ( )

№ п/п
1	0
2	3
3	6
4	9
5	12
.	.
.	.
.	.
.	.

7 ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Темп охлаждения (m) определяется как результат графической обработки регулярной стадии зависимости   по формуле (3.8). Поскольку избыточная температура (υ) прямопропорциональна значению термо ЭДС, измеряемому прибором, то

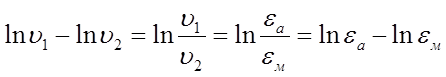
Поэтому для расчёта темпа охлаждения не требуется производить пересчёт термо ЭДС в температуру.

Опыт № 1

7.1.1  Рассчитать lnυ_a и lnυ_м в процессе выравнивания температур для каждого значения (τ).

7.1.2  Построить графики зависимости lnυ_м=f(τ) и lnυ_a=f(τ) в одной системе координат.

7.1.3  Для каждого из графиков lnυ=f(τ) определить интервал времени, соответствующий линейной зависимости lnυ=lnε=c=mτ, то есть регулярному режиму.

7.1.4  По линейным участкам зависимости lnυ=f(τ) рассчитать темп нагревания для медного образца (m_м) и для ампулы (m_a) по формуле:

 

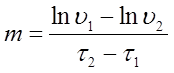                                                                                 ,                                              (7.13)

7.1.5  В соответствии с (3.10), по темпу нагревания медного образца (m_м) рассчитать коэффициент теплоотдачи (α):

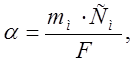
                                                                                                               (7.14)

где С_м=с_м·М_м – полная массовая теплоёмкость медного образца;

      с_м – удельная теплоёмкость меди;

      М_м – масса медного образца;

      F – площадь поверхности образца;

F_м=2·π·R_м·(R_м+h_м), [     ],

 где R_м – радиус медного цилиндра;

       h_m– высота медного цилиндра.

7.1.6  Темп охлаждения ампулы с исследуемым веществом в условиях

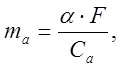также определяется параметрами :

                                                                               [с^-1]

где С_а – полная массовая теплоёмкость ампулы с исследуемым веществом.

Поскольку форма и размеры ампулы  и медного образца одинаковы, а также одинаковы условия, в которых они находятся, то можно считать, что коэффициенты теплоотдачи при нагревании ампулы и меди одинаковы. Если при этом одинаковы и площади поверхности обоих образцов, то справедливо равенство:

 

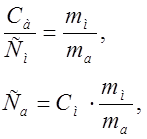                                                                       тогда

(7.15)

но полная массовая теплоёмкость ампулы складывается из массовой теплоёмкости оболочки и исследуемого вещества:

                                                                                                                   (7.16)

где c_o – удельная теплоёмкость оболочки;

     М_о – масса оболочки;

     с – удельная теплоёмкость исследуемого вещества, заполняющего оболочку;

     М – масса исследуемого вещества;

Из (7.15) и (7.16) получаем:

 

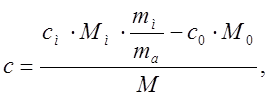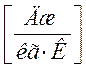                                                                                                                   (7.17)

Опыт № 2