









Министерство Образования Российской Федерации
Филиал ГОУВПО
«Московский энергетический институт
(технический университет)»
в г.Волжском
Кафедра промышленной теплоэнергетики
Лабораторная работа №1
по курсу термодинамики
Определение показателя адиабаты воздуха
Студент Парасоцкий А.Б.
Группа АТП-02
Преподаватель Шевцова С.Б.
Волжский 2004
1. Цель работы
Экспериментальное
определение показателя адиабаты ![]() для воздуха.
для воздуха.
2. Теоретические основы работы
Адиабатным (адиабатическим) называют термодинамический процесс, происходящий в термодинамической системе без подвода теплоты. Первое начало термодинамики для произвольного термодинамического процесса имеет вид:
![]() (1.1)
(1.1)
Где
![]() - бесконечно малое количество теплоты,
подводимое к термодинамической системе;
- бесконечно малое количество теплоты,
подводимое к термодинамической системе;
![]() - бесконечно малое изменение внутренней
энергии системы;
- бесконечно малое изменение внутренней
энергии системы;
![]() - бесконечно малая работа, совершаемая
термодинамической системой в результате данного процесса.
- бесконечно малая работа, совершаемая
термодинамической системой в результате данного процесса.
Для адиабатного процесса (1.1) принимает вид:
![]() (1.2)
(1.2)
Для одного моля идеального газа справедливы соотношения:
![]() , (1.3)
, (1.3)
![]() . (1.4)
. (1.4)
Здесь ![]() - молярная теплоёмкость при постоянном
объёме газа;
- молярная теплоёмкость при постоянном
объёме газа;
![]() - давление;
- давление;
![]() - бесконечно малое изменение температуры.
- бесконечно малое изменение температуры.
![]() - бесконечно малое изменение объёма.
- бесконечно малое изменение объёма.
Подставляя (1.3) и (1.4) в (1.2), получим:
![]() (1.5)
(1.5)
Для одного моля идеального газа запишем уравнение Клапейрона:
![]() ;
;
R – газовая постоянная.
Дифференцируя
его, найдём связь между ![]() ,
, ![]() и
и ![]() :
:
![]() ; (1.6)
; (1.6)
Из (1.6) получим:
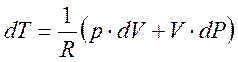 ; (1.7)
; (1.7)
Подставляя (1.7) в (1.5), получим дифференциальное уравнение, связывающее объём и давление идеального газа в адиабатном процессе:
![]() . (1.8)
. (1.8)
Учитывая,
что ![]() - молярная теплоёмкость идеального газа
при постоянном давлении, и вводя обозначение:
- молярная теплоёмкость идеального газа
при постоянном давлении, и вводя обозначение:
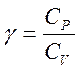 , (1.9)
, (1.9)
из (1.8) получим:
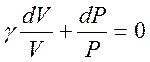 (1.10)
(1.10)
Известно,
что для идеального газа ![]() и
и ![]() не зависят от температуры:
не зависят от температуры:
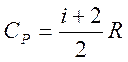 ;
; 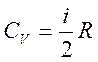 (1.11)
(1.11)
(i – число степеней свободы молекулы идеального газа);
Считая
воздух при атмосферном давлении идеальным газом, получаем, что ![]() для данного газа величина. В этом случае
решение дифференциального уравнения (1.10) имеет вид:
для данного газа величина. В этом случае
решение дифференциального уравнения (1.10) имеет вид:
![]() (1.12)
(1.12)
(1.12)
называют уравнением адиабаты (уравнением Пуассона), а показатель ![]() - показателем адиабаты (показателем
Пуассона).
- показателем адиабаты (показателем
Пуассона).
3. Описание установки и вывод расчётных формул
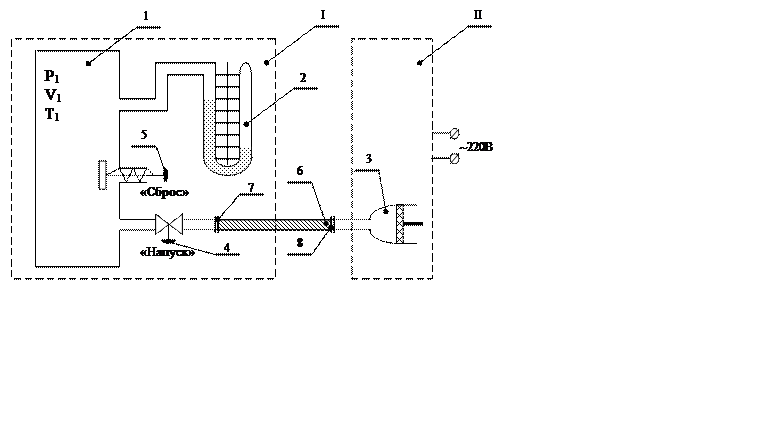
Рис. 3.1
I – Лабораторный модуль
II – Приборный модуль;
1 – Баллон;
2 – Манометр;
3 – Компрессор;
4 – Клапан «Напуск»;
5 – Клапан «Сброс»;
6 – Соединительный шланг;
7 – Штуцер пневмопровода;
8 – Штуцер компрессора.
Экспериментальная установка (Рис. 3.1) состоит из:
I – лабораторного модуля (ЛМ) и II– приборного модуля (ПМ).
ЛМ
состоит из баллона (1), наполненного воздухом. Баллон соединён с манометром
(2). Через клапан (4) «напуск» и через резиновый шланг (6) баллон соединён с
компрессором (3) приборного модуля. Клапан (5) предназначен для соединения баллона
(1) с атмосферой, а так как его поперечное сечение достаточно велико, то
процесс установления атмосферного давления в сосуде происходит достаточно
быстро. Изменение давления происходит практически без теплообмена с окружающей
средой, поэтому процесс можно считать адиабатным. С помощью насоса (3) в баллон
(2) накачали воздух, затем закрыли кран (4). Через несколько минут температура
воздуха в баллоне станет равной температуре в лаборатории. Обозначим эту
температуру ![]() . Давление в баллоне
. Давление в баллоне ![]() при этом равно:
при этом равно:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.